Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 06. 04. 2013 17:27 — Editoval frantax (06. 04. 2013 17:29)
Re: Integrál
↑ byk7:
Jo diky, to sem si taky rikal ale nevim jakou a nevidim tam nikde derivaci toho integralu..
Ja ve skole ty integraly uplne zaspal a pak sem se je doucoval z ucebnice krynickeho, ale s tady timhle stejne nemuzu hnout :D , a to se musim jeste nekde naucit integrova ty ruzne lomene a jine fce..
Offline
#7 06. 04. 2013 18:31 — Editoval byk7 (06. 04. 2013 18:31)
Re: Integrál
↑ frantax:
Jak už jarrro napsal, tak máš
a toto musíš zintegrovat per partes.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#8 06. 04. 2013 18:35
Re: Integrál
↑ frantax:per partes derivovať  , ale dá sa aj tak ako ↑ byk7: to je jedno
, ale dá sa aj tak ako ↑ byk7: to je jedno
MATH IS THE BEST!!!
Offline
#10 06. 04. 2013 19:10
Re: Integrál
↑ frantax:tak potrebuješ zistiť čomu sa rovná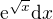
za podmienky, že
potom 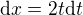
ďalej je to len dosadenie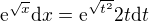
MATH IS THE BEST!!!
Offline
 ?
? 
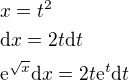
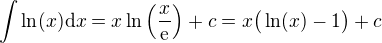

 jsi se dostla tak ze jakoby vynasobis ten druhy radek *
jsi se dostla tak ze jakoby vynasobis ten druhy radek * 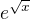 nebo jak to mam pochopit ?
nebo jak to mam pochopit ?