Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 04. 2013 00:52 — Editoval Honza90 (07. 04. 2013 01:44)
vnější součin a vnější algebra
Dobrý den. Chtěl bych si jen ujasnit konstrukci vnější(exterior) algebry vektorového prostoru, jestli se to tak dá nazývat. Vnější součin vektorů  je definován jako
je definován jako 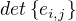 a
a
to lze chápat jako bivektor, který sám o sobě je prvkem báze prostoru 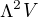 který je sám vektorovým prostorem. Teď tuším, že by
který je sám vektorovým prostorem. Teď tuším, že by 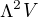 měl být uzavřený na násobení, aby se jednalo o algebru.
měl být uzavřený na násobení, aby se jednalo o algebru.
Tedy, jeli  dimenze 3, pak báze
dimenze 3, pak báze 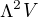 je
je 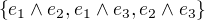
Teď nevím, jestli to násobení je opět ten "wedge" nebo jak je definované
protože 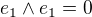 tak by to celé bylo nula, ale to se mi nezdá. Ano jsou to ortogonální prvky, takže jejich skalární součin by měl být nula, ale
tak by to celé bylo nula, ale to se mi nezdá. Ano jsou to ortogonální prvky, takže jejich skalární součin by měl být nula, ale  a e1,e2 jsou taky ortogonální.
a e1,e2 jsou taky ortogonální.
Pomůže mi někdo do toho trochu proniknout? Díky :)
EDIT: Našel jsem poučku, která tvrdí, že pokud součet "řádů" násobených prvků, v tomto případě 2 + 2 je větší než dimenze  (ta je 3) pak wedge těchto dvou bude 0 jak jsem napsal. Takže aspoň vím, že tady už se
(ta je 3) pak wedge těchto dvou bude 0 jak jsem napsal. Takže aspoň vím, že tady už se 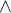 chová jinak. Na tomto prostoru by měl být zaveden ještě nějaký skalární součin, ale nedaří se mi rozlousknout jeho definici.
chová jinak. Na tomto prostoru by měl být zaveden ještě nějaký skalární součin, ale nedaří se mi rozlousknout jeho definici.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#2 07. 04. 2013 02:43 — Editoval Brano (07. 04. 2013 02:45)
Re: vnější součin a vnější algebra
 netvori algebru ale iba jej cast. Grasmannova algebra je
netvori algebru ale iba jej cast. Grasmannova algebra je
resp.
http://en.wikipedia.org/wiki/Exterior_algebra
Offline
#4 07. 04. 2013 03:37 — Editoval Brano (07. 04. 2013 23:33)
Re: vnější součin a vnější algebra
zakladna pointa je v tom, ze  je izomorfne s
je izomorfne s 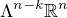 (maju rovnaku dimenziu) a
(maju rovnaku dimenziu) a  je ten izomorfizmus; napr. medzi
je ten izomorfizmus; napr. medzi 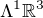 a
a  je prirodzene ho definovat tak, ze
je prirodzene ho definovat tak, ze 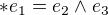 ,
,  ,
, 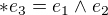 a potom si mozes vsimnut, ze ak
a potom si mozes vsimnut, ze ak  potom
potom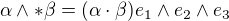
pozor: mozu byt rozne konvecie co by sa lisili v znamienku alebo konstante
vzdy plati  cize de facto konstanta, takze to definuje "skalarny sucin"
cize de facto konstanta, takze to definuje "skalarny sucin"
Offline
#7 07. 04. 2013 23:29
Re: vnější součin a vnější algebra
↑ Brano:
jasne, ja myslel ze  znaci celou algebru. Takze skalarny soucin mezi vektory jineho ranku proste neni definovan, nebo je automaticky 0? Pak jsem jeste premyslel jestli existuje neco jako identita k wedge productu:
znaci celou algebru. Takze skalarny soucin mezi vektory jineho ranku proste neni definovan, nebo je automaticky 0? Pak jsem jeste premyslel jestli existuje neco jako identita k wedge productu: ?
?
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#8 07. 04. 2013 23:32 — Editoval Brano (07. 04. 2013 23:40)
Re: vnější součin a vnější algebra
↑ Honza90:
aha vidis to, moja chyba, popridavam tam tie jednotky do mocnin ..
jednotka wedge produktu je normalne konstanta  lebo ak
lebo ak  je konstanta, tak
je konstanta, tak 
a skalarny sucin vektorov ineho ranku sa myslim obvykle nedefinuje (hlavny problem by mohol byt aj to, ze su s podpriestorov s inymi dimenziami)
Offline

 pak
pak  ,
, 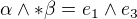 a to není
a to není 
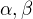 musí být oba k-vektory jinak to neplatí
musí být oba k-vektory jinak to neplatí (t.j. rovnake
(t.j. rovnake 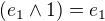 , když třeba
, když třeba  tak to pak nebude vnější součin v pravém slova smyslu, když
tak to pak nebude vnější součin v pravém slova smyslu, když