Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 02. 2012 20:09
- FlyingMonkey
- Příspěvky: 758
- Reputace: 4
Slovní úloha
Dobrý večer,
tak si projíždím nějaké slovní úlohy a mám problém vlastně se všemi :D
Zadání:
"Posadí-li se do každé lavice kromě poslední 7 žáků, zbude pro poslední lavici jen jeden žák. Jestliže se do každé lavice posadí 6 žáků, nezbude pro jednoho žáka místo. Kolik je všech žáků?"
Já asi ani pořádně nerozumím tomu zadání ... Jakože 1 lavice = 7 žáků?
Zkusil jsem si to vyjádřit rovnicemi:
y ... počet žáků
x ... počet lavic
Radši to popíšu slovy, abyste mi to mohli líp vymluvit :D
Do každé lavice 7 žáků, to znamená, že tam bude 7x + 1 žáků, right?
y = 7x + 1
V druhém případě:
počet žáků bude každá lavice * 6, ale pro jednoho nezbude místo a to nevím, jak zapsat ... :/ zase bych tam asi přičetl prostě 1, protože 1 jakoby přebývá... ale to je asi blbost :)
y = 6x + 1
Díky za pomoc ! :)
Offline
- (téma jako vyřešené označil(a) FlyingMonkey)
#2 02. 02. 2012 20:18 — Editoval Aquabellla (02. 02. 2012 20:27)
- Aquabellla
- Moderátorka Bellla
- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Slovní úloha
↑ FlyingMonkey:
1) y = 7x + 1
2) y = 6(x + 1) + 1
V prvním případě je plně zaplněno o jednu lavici méně než ve druhém :-)
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 02. 02. 2012 20:22
- zlomenavetev
- Příspěvky: 34
- Pozice: Student
- Reputace: 0
Re: Slovní úloha
Já bych napsal:
první rovnice - y=7x-1
druhá rovnice - y = 6x+1
x = 2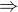 
y - 7 . 2 -1 = 13
nejsem si jistý, zda je to správně
Offline
#4 02. 02. 2012 20:24
- zlomenavetev
- Příspěvky: 34
- Pozice: Student
- Reputace: 0
Re: Slovní úloha
↑ zlomenavetev:
takže to mám blbě ;)
Offline
#5 02. 02. 2012 20:55
- FlyingMonkey
- Příspěvky: 758
- Reputace: 4
Re: Slovní úloha
Aqua - Díky :)
Jenom asi nechápu jaktože je v druhé o jednu víc plně zaplněnou? Můžu poprosit ještě trochu o objasnění? :)
a pak to y = 6(x+1) + 1
si asi nedokážu úplně odůvodnit, ani zpětně, můžu poprosit, jak se k tomu došlo? :)
Jakože mám 6 žáků do jedné lavice to chápu, ale proč k tomu přičítám ještě 6? tu jedničku tam chápu, to je ten přebývající ...
Díky moc za pomoc :)
Zlomenavetev - nevadí, díky za reakci ;)
Offline
#6 02. 02. 2012 21:01
- Aquabellla
- Moderátorka Bellla
- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Slovní úloha
↑ FlyingMonkey:
"Posadí-li se do každé lavice kromě poslední 7 žáků, zbude pro poslední lavici jen jeden žák. Jestliže se do každé lavice posadí 6 žáků, nezbude pro jednoho žáka místo. Kolik je všech žáků?"
Počet lavic je (x + 1). Počet žáků je y.
1) "do každé lavice kromě poslední - 7 žáků": 7(x + 1 - 1) = 7x
"v poslední lavici je jeden": 1
--> dohromady y = 7x + 1
2) "v každé lavici 6 žáků": 6(x + 1)
"na jednoho žáka nezbude místo": 1
--> y = 6(x + 1) + 1
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#7 02. 02. 2012 21:12
- FlyingMonkey
- Příspěvky: 758
- Reputace: 4
Re: Slovní úloha
Oky, tomu zápisu rozumím, díky :), ale když se to snažím vypočítat, tak mi to nevychází ..
prostě y z 2) hodím do 1) a dostanu 7x + 7 = 7x + 1 ... což jak je vidět nevede k výsledku :)
že bych neuměl řešit soustavu? :D
Díky
Offline