Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » druhá derivace konvexní funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 04. 2013 20:00
druhá derivace konvexní funkce
Ahoj,
potřebovala bych poradit s tímto problémem:
Mám konvexní funkci f a vím, že existuje její první derivace, která je nezáporná. Můžu předpokládat, že existuje i druhá derivace funkce f?
Budu ráda za jakoukoliv pomoc:)
Offline
- (téma jako vyřešené označil(a) drabi)
#5 09. 04. 2013 21:30
Re: druhá derivace konvexní funkce
↑ Stýv:
Dobře. Chtěla jsem dokázat, že mám-li distribuční funkci F konvexní na intervalu ![kopírovat do textarea $(-\infty,m]$](/mathtex/3d/3dc3e8a662fde08c311d38bd5f5115bb.gif) a konkávní na
a konkávní na 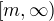 , pak f = F' je rostoucí
, pak f = F' je rostoucí ![kopírovat do textarea $(-\infty,m]$](/mathtex/3d/3dc3e8a662fde08c311d38bd5f5115bb.gif) na a klesající na
na a klesající na 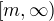 .
.
f je hustota a je nezáporná. Lze toto nějak dokázat?
Offline
#6 10. 04. 2013 12:28
Re: druhá derivace konvexní funkce
↑ drabi:
Myslím, že ne - konstantní funkce je totiž konkávní i konvexní současně a na intervalech, kde je distribuční funkce konstantní,je konstantní i hostota. Ale slabší tvrzení kde se místo rostoucí resp. klesající použije neklesající resp. nerostoucí, je myslím v pořádku.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#7 10. 04. 2013 12:37
Re: druhá derivace konvexní funkce
↑ martisek:
Díky za odpověď.
S tou nerostoucí/neklesající bych se nejspíš spokojila. Ale jak toto dokázat? Mohl bys mi prosím poradit?
Offline
#8 11. 04. 2013 17:21
Re: druhá derivace konvexní funkce
tak tedy pro zájemce jsem konečně dala dohromady důkaz:
Distribuční funkce  je na intervalu
je na intervalu ![kopírovat do textarea $(-\infty,m]$](/mathtex/3d/3dc3e8a662fde08c311d38bd5f5115bb.gif) konvexní.
konvexní.
Pro každé ![kopírovat do textarea $x,y \in (-\infty,m]$](/mathtex/32/32f3b8f98d760b443fe052fbf06e4685.gif) a pro každé
a pro každé ![kopírovat do textarea $\lambda \in [0,1]$](/mathtex/48/482bc88665ac9397fb018d1e29edec1d.gif) tedy platí
tedy platí ![kopírovat do textarea $F[\lambda x + (1-\lambda)y] \leq \lambda F(x) + (1-\lambda) F(y)$](/mathtex/b3/b33573400c5a702bc8077dcb1aacf7f5.gif) . (*)
. (*)
Nech  . Nech
. Nech  je hustota
je hustota  , potom platí vztah
, potom platí vztah 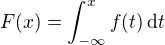 .
.
Dosadíme-li do (*) dostáváme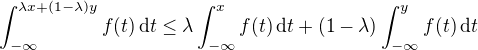
Volíme 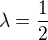 a upravujeme
a upravujeme
Pro spor předpokládejme, že funkce  je klesající. Potom platí
je klesající. Potom platí
Na obou stranách ostré nerovnosti máme stejný výraz, což je spor. Tedy funkce  je neklesající.
je neklesající.
Stejným způsobem lze dokázat, že je-li  konkávní, pak
konkávní, pak  je nerostoucí.
je nerostoucí.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » druhá derivace konvexní funkce (TOTO TÉMA JE VYŘEŠENÉ)


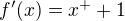 splňuje tvoje předpoklady, ale nemá druhou derivaci v 0
splňuje tvoje předpoklady, ale nemá druhou derivaci v 0