Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 04. 2013 20:03
Kondezatory
Zdravím. Kondenzátory - C1,C2,C3. C1 a C3 jsou spojeny paralelně a pak jsou sériově připojeny k C2. C1 a C2 jsou nastavitelné (vzdálenost jejich desek se může měnit), C3 má vzdálenost desek D a kapacitu C. Když se C1 a C2 nastaví taky na vzdálenost D, mají také kapacitu C. Na jakou vzdálenost se musí nastavit desky C1 a C2, aby kapacita celkového obvodu byla 2C? Postupoval jsem takhle.. spocital jsem si napred kapacitu, jako by vsechny meli stejne parametry. Mozna by nebylo spatny pouzit  . Tusim ze tu bude urcite nejaky trik. Prosim, jak na to?
. Tusim ze tu bude urcite nejaky trik. Prosim, jak na to?
Offline
#2 11. 04. 2013 20:38
Re: Kondezatory
Také zdravím. Ty kondenzátory 1,2 se mají nastavit na stejnou vzdálenost, nebo různou? Ono na tom vlastně nezáleží, buďto budeš řešit normální kvadratickou rovnici, nebo kvadratickou rovnici s parametrem.
Když si spočítáš kapacitu, kdy jsou všechny stejné jako 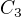 , tak by mělo vyjít
, tak by mělo vyjít  . Potom, když budeme uvažovat
. Potom, když budeme uvažovat  , řešíme rovnici
, řešíme rovnici .
.
To mi bohužel nevychází vůbec pěkně: .
.
Teprve nyní se použijeme vztah mezi vzdáleností desek a kapacitou, takže máme

Kdyby d(C1) a d(C2) byly různé, tak by u rovnice vyšel vztah mezi nimi. Nicméně ta odmocnina z prvočísla se mi vůbec nelíbí, takže jsem se možná někde přepočítal.
ŘEŠTE FYKOS!
Offline
#3 11. 04. 2013 20:46 — Editoval SoniCorr (11. 04. 2013 20:54)
Re: Kondezatory
ja jsem to zkousel takhle... kdyz jsem si to spocital kolik to ma kapacitu bez uprav, tak jsem si to oznacil jako treba c s carkou u tebe C=2/3C3... C1=C2 to me tez napadlo a ted jsem udelal to, ze to chci upravit nejak a nahradil jsem C a carkou jako 2C. akorat nejsme schopny vyresit :D jo a jeste jsem si oznacil C3 jako C.. radeji to napisu  a jeste budu potrebovat zmensit vzdalenost ne? abych zvetsil kapacitu
a jeste budu potrebovat zmensit vzdalenost ne? abych zvetsil kapacitu
Offline
#5 11. 04. 2013 21:38
Re: Kondezatory
↑ SoniCorr:
Obávám se, že tu rovnici nemáš sestavenou dobře. Jestliže máš celkovou kapacitu nové soustavy  a původní tedy
a původní tedy  , tak nemůžeš na pravé straně rovnice psát
, tak nemůžeš na pravé straně rovnice psát  místo
místo 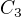 , protože
, protože  .
.
ŘEŠTE FYKOS!
Offline
#6 11. 04. 2013 22:07
Re: Kondezatory
C je kapacita kondezatoru ( jednoho) a ted chceme 2C a to co si napsal je nejaky C jiny ( pro me s carkou)... aspon takhle to chapu ja. a v zadani po me chcou kapacitu o hodnote dvou kondezatoru o hodnotach C a D podle zadani... ono je to zadani celkove zvlastni
Offline
