Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#2 14. 04. 2013 14:19
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: Limita posloupnosti
Vytkni si nejdriv 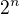 a pak jsi vytkni
a pak jsi vytkni  . Ma pak vyjit
. Ma pak vyjit  . Wolfram dava za pravdu.
. Wolfram dava za pravdu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
 ¨
¨
