Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2013 20:35
konštntná gravitačná sila
Raz som tak rozmýšlal a napadlo ma že keďže gravitácia je priamo úmerná hmotnosti a nepriamo úmerná štvorcu vzdialenosti A hmotnosť je je priamo úmerná rýchlosti tak by ASI mala existovať nejaká funkcia dráhy od času pri ktorej by vzhľadom na aktuálnu vzdialenosť a rýchlosť bola sila rovnaká ako na začiatku merania. čiže: 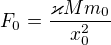
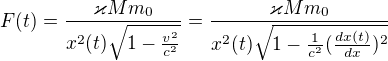
takže logicky: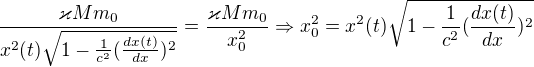
čo som ,,upravil" na tvar :![kopírovat do textarea $[\frac{x_{0}}{x(t)}]^{4}=1-(\frac{x´(t)}{c})^{2}$](/mathtex/d6/d650731373c3613c33c693addcae00f6.gif)
a hodil wolframovi ktorý mi vyplul:
http://www.wolframalpha.com/input/?i=%2 … %2Fb%29**2
1. Je tá myšlienka o konštantnej gravitácii vôbec správna?
2. Dobrá rovnica? Dobre upravená?
3. Čo je to za riešenie?
Offline
#2 16. 04. 2013 10:26 — Editoval found (16. 04. 2013 11:55)
Re: konštntná gravitačná sila
↑ riders21:
Ahoj, já nejsem nijaký relativistický expert, tak nečekej zázraky z mého příspěvku. :)
Prvně bych podotkl, že to není úplně přímá úměra mezi hmotností a rychlostí (viz graf dole).
Co se toho dalšího týče, asi to nezní úplně špatně. Samozřejmě je tu problém v tom, že na úrovni rychlostí, na kterých se projevuje relativistické působení na hmotnost, už neplatí Newtonův gravitační zákon (alespoň co vím). Kdybychom předpokládali platnost, tak si stejně myslím, že takovou rychlostí bude sotva kdy něco padat, abychom dostali nějaký možný výsledek. To vše za předpokladu, kdy je hmotnost závislá na čase dle daného vzorce, a dále kde pro lib. rychlosti platí Newtonův gravitační zákon - uvažujme, že jsme v takovém vesmíru.
A co se toho samotného výpočtu týče, tam můžeme odmocninu brát jako funkci 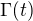 , ať nám to nijak víc žíly netrhá. Ty jsi dostal určitý výsledek jako
, ať nám to nijak víc žíly netrhá. Ty jsi dostal určitý výsledek jako 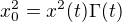 . Tak, co od toho očekávat. Prvně to, že
. Tak, co od toho očekávat. Prvně to, že  vypovídá o tom, že
vypovídá o tom, že  pro obě hodnoty větší než 1 (ať je to hezčí), tedy že by těleso bylo blíže před působením síly než po pohybu směrem k centru - not so good pro přitažlivou sílu. Taky si dej pozor na to, že derivuješ podle času a ne podle x (a prakticky tam tu derivace vůbec psát nemusíš, stačí psát normálně rychlost). Dostáváš se tedy do sporu s předpokladem, že síla je přitažlivá (pokud jsi takový měl), čímž by mělo být vyvráceno, že existují dvě takové polohy se stejnou silou.
pro obě hodnoty větší než 1 (ať je to hezčí), tedy že by těleso bylo blíže před působením síly než po pohybu směrem k centru - not so good pro přitažlivou sílu. Taky si dej pozor na to, že derivuješ podle času a ne podle x (a prakticky tam tu derivace vůbec psát nemusíš, stačí psát normálně rychlost). Dostáváš se tedy do sporu s předpokladem, že síla je přitažlivá (pokud jsi takový měl), čímž by mělo být vyvráceno, že existují dvě takové polohy se stejnou silou.
V další části máš někde chybu v sázení, takže nevím, co's tam chtěl napsat, ale myslím, že už předešlý výsledek by měl experimentálně padnout, jak když si zkusíš nechat padat tužku a zjistíš, že neletí vzhůru. Ten vesmír, ve kterém jsi to počítal, určitě nebude náš (a bude dost zvrhlý).
J.
A viz k úměře graf:
Edit: Ještě mě tak zpětně napadá, že pokud máš sílu, která ubývá s x^2 a vyjádříš si sílu ve tvém pojetí, tak dostáváš úměrnost na způsob
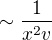 .
. Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
