Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2013 16:11
priklady kmity
1.príklad
Atómy v pevných látkach kmitajú za pokojovej teploty (T=20°C)s frekvenciou rádovo 10 THz (terahertzov. Vychádzajme z predstavy atómov prepojených pružinami. Predpokladajme, že v telese zo striebra kmitá jeden atóm striebra s uvedenou frekvenciou a ostatné atómy sa nepohybujú. vypočítajte tuhosť pružiny. Jeden mól striebra je 6,23*10^23 častíc a váži 108 gramov.
2.príklad
Daná častica harmonicky kmitá s frekvenciou 0,25 Hz okolo rovnovážnej polohy x = 0. V čase t=0 mala výchylku x=0,37 cm a nulovú rýchlosť. Určte pre jej kmitanie:
a)periódu, b) uhlovú frekvenciu (omega), c) amplitúdu, d) výchylku ako funkciu času, e) rýchlosť ako funkciu času, f) maximálnu rýchlosť,
g) maximálne zrýchlenie, h) výchylku v čase t = 3,0 s, i) rýchlosť v čase t = 3,0 s
Offline
- (téma jako vyřešené označil(a) winner123)
#2 16. 04. 2013 10:20
Re: priklady kmity
↑ winner123:
1.
Platí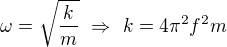
Když 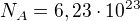 atomů má hmotnost
atomů má hmotnost 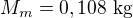 , tak jeden atom má hmotnost
, tak jeden atom má hmotnost 
Je tedy 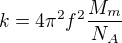
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 17. 04. 2013 12:34
Re: priklady kmity
↑ winner123:
2) to jsou jen vzorečky - můžeš najít v každé učebnici
a) 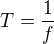
b) 
c) Podle zadání je 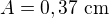
d) 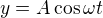
e) 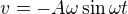
f) 
g) 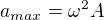
h) 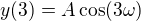
i) 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
