Matematické Fórum

direwolf · 20. 04. 2013 12:27

$2x^{2}+3kx+k^{2}+2a+1=0$

Počítám slovní úlohu a v řešení jsem dospěl k výše uvedené rovnici a nevím si s ní rady. Mohl by mi s ní někdo prosím pomoct? Předem mockrát děkuji!

found · 20. 04. 2013 12:34

Ahoj,

v čem přesně je problém, pokud bys chtěl spočítat diskrinant a určit podmínky, kdy rovnice má řešení a kdy ne? Za sebe osobně dostat tuhle rovnici, tak napíši

$D = 9k^2 - 8(k^2 + 2a+ 1) = k^2 + 16a - 8$

$D = 0 \Leftrightarrow a = \frac{8-k^2}{16} \Leftrightarrow k = \pm\sqrt{8 - 16a}$

Popřípadě pro řešení s odpovídajícími nerovnostmi pro existenci dvou řešení (D > 0) či neexistenci žádného řešení (D<0). Nicméně ty máš v zadání té slovní úlohy asi něco zjistit, ne? To by se hodilo vědět, na co vlastně máš přijít. ;)

direwolf · 20. 04. 2013 12:35

Zapomněl jsem dodat, že $k$ a $a$ jsou parametry.

direwolf · 20. 04. 2013 12:42

Ano k tomuto jsem došel taky, jenže mám ještě řešit případy, kdy 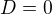$D=0$ a $D>0$ a $D<0$ .
Původní zadání úlohy je:
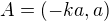Na parabole $y=kx-x^{2}$ nalezněte souřadnice bodu R, který je nejbližší k bodu $A=(-ka,a)$ . Určete také tuto vzdálenost.
Z tohoto zadání jsem si obecně vypočítal, jaká by byla vzdálenost bodu R a A a tento výraz zderivoval a položil roven nule, až jsem se dostal k této rovnici.

jelena · 20. 04. 2013 13:49

Zdravím v tématu,

zkusím pokračovat v postupu kolegy ↑ found: dle návrhů kolegy ↑ direwolf:. Máme D=f(a, k) a potřebujeme vyšetřit, pro které a, k funkce má případy 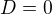$D=0$ , $D>0$ , $D<0$ .

$D = k^2 + 16a - 8=(k+2\sqrt{2(2a-1)})(k-2\sqrt{2(2a-1)})$

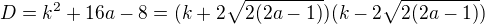
Máme přepsáno do součinu a vyšetříme, kdy je součin kladný, záporný nebo nulový (+podmínky pro výraz pod odmocninou). Prakticky si představuji tak, že kladný D odpovídá 2 řešení rovnice, co sestavil kolega ↑ direwolf: (pokud zadaný bod A leží na ose souměrnosti paraboly, máme 2 body stejně vzdálené) a nulový D odpovídá jinému umístění bodu A vůči parabole (jen jeden bod stejně vzdálený). Uvažuji, v kterém umístění A se promítne záporné D?

Samotný postup k řešení jsem neověřovala, začátek byl rozpracován zde.

direwolf · 20. 04. 2013 15:44

A mohl bych se prosím ještě zeptat, jak ověřím, že dané stacionární body (tzn. možné kořeny výše uvedené kvadratické rovnice, když D=0 a D>0) jsou i globální extrémy funkce?

jelena · 20. 04. 2013 18:37

↑ direwolf:

já bych ověřovala přes znaménko 2. derivaci v bodě podezřelém z extrému.

Matematické Fórum

#1 20. 04. 2013 12:27

kvadratická rovnice se dvěma parametry

#2 20. 04. 2013 12:34

Re: kvadratická rovnice se dvěma parametry

#3 20. 04. 2013 12:35

Re: kvadratická rovnice se dvěma parametry

#4 20. 04. 2013 12:42

Re: kvadratická rovnice se dvěma parametry

#5 20. 04. 2013 13:49

Re: kvadratická rovnice se dvěma parametry

#6 20. 04. 2013 15:44

Re: kvadratická rovnice se dvěma parametry

#7 20. 04. 2013 18:37

Re: kvadratická rovnice se dvěma parametry

Zápatí