Matematické Fórum

souteh · 19. 04. 2013 23:14

Prosím o vysvětlení postupu.

Oxyd · 20. 04. 2013 01:25

Dosadíš $a$ ] a 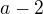$a - 2$ za $x$ do definice $f$ , dostaneš tak kvadratickou nerovnici, tu upravíš na tvar (a - něco)(a - něco jiného) < 0 a tu vyřešíš rozborem případů. (Při tom dosazování nezapomeň na závorky.)

Zkus nám radši ukázat, kam ses až dostal a co ti kde není jasné.

souteh · 20. 04. 2013 15:42

Tzn. $a^{2}-3(a-2)<10$ ?

Nepochopil jsem vůbec tu spojitost mezi $x$ a $a$ ..

jelena · 20. 04. 2013 21:01

↑ souteh:

Zdravím,

to je populární úloha z přijímaček VŠE. Funkce f(x) má jasný předpis, pro konkrétně zadanou hodnotu x (např. x=7) umíš dosadit a vypočíst hodnotu f(7)=... Stejně tak umíš vypočíst hodnotu od x=7-2 (což je od x=5). V úloze však nemáš konkrétní hodnotu x=číslo, ale je zadán parametr a. Tak ho pořádně (to jsi neprovedl) dosazuješ do předpisu místo x.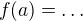

$f(a)=\ldots$ ,
$f(a-2)=\ldots$

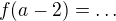
Potom všechno sepíšeš do nerovnice. Podaří se pokračovat (a je jasná spojitost mezi $x$ , $a$ a "sadovým ovocem" (c))? Děkuji.

souteh · 20. 04. 2013 22:51

Kouknul jsem na to předchozí téma a vyšlo mi toto:

$(a^{2}-3a)-[(a-2)^{2}-3(a-2)]<10$
$a^{2}-3a-(a^{2}-4a+4-3a+6)<10$
$a^{2}-3a-a^{2}+4a-4+3a-6<10$
$4a<20$
$a<5$
$a\in (-\infty ;5)$

???