Matematické Fórum

Dinula · 20. 04. 2013 10:03

Zdravím,
prosím může mi někdo pomoci s tímto příkladem?

$\int_{0}^{e-1} ln(x+1)dx$

found · 20. 04. 2013 10:21 — Editoval found (20. 04. 2013 10:23)

Ahoj,

doporučil bych per partes, kdy funkce u = ln(x+1) a druhá funkce bude v' = 1. Jedná se vlastně o trik pro PerPartes, kdy vezmeš celou funkci jako u a tu vynásobíš jedničkou, potom tu jedničku pokládáš za v'. Užívá se to takhle u logaritmů s lineárním argumentem (možná by se to dalo použít i jinde, ale zatím jsem se s tím nesetkal - takže tu metodu neházej jen na logaritmy). Finálně se tím dostane

$\int_0^{e-1} \ln(x+1) dx = \left[x\ln(x+1)\right]_0^{e-1} - \int_0^{e-1}\frac{x}{x+1}dx.$

Tohle už bys zvládl?

J.

Dinula · 20. 04. 2013 10:34

↑ found:
Tak o tom jsem ještě ani neslyšela :D
Mohla bych poprosit ještě o větší nápovědu? Matika opravdu není moje kamarádka, byla bych vám moc vděčná

jarrro · 20. 04. 2013 10:42

↑ Dinula:akú väčšiu je predsa
$\frac{x}{x+1}=1-\frac{1}{x+1}$

found · 20. 04. 2013 11:08 — Editoval found (20. 04. 2013 11:12)

↑ Dinula:

Tak jak praví kolega ↑ jarrro:. Jen ještě dodám, že kdybys nevěděla, proč to tak je, tak to vychází z následující vlasnosti: 0 = 1 - 1:

$\frac{x}{x+1} = \frac{x + 0}{x+1} = \frac{x + 1 - 1}{x+1} = \frac{x+1}{x+1} - \frac{1}{x+1} = 1 - \frac{1}{x+1}$

Tenhle trk si také zapamatuj, já ho třeba pro výpočet integrálů používal často, když to šlo. Povětšinou u racionálních funkcí (podíly polynomů) se dá složitý výraz převést na několik snazších - nemusí se přitom jednat jen o 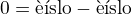$0 = \text{číslo} - \text{číslo}$ , ale může se tam objevit i proměnná: 0 = x - x; $0 = x^2 - x^2$ .

J.

user · 21. 04. 2013 02:57

Ahoj,
druhý integrál není potřeba počítat, stačí využít "triku" v per partes. Položíš v'=1 a v=x+1. K integrované funkci lze libovolně přičíst konstantu. Místo $\int \frac{x}{x+1}\text{d}x$ dostaneš $\int 1\text{d}x$ .

Matematické Fórum

#1 20. 04. 2013 10:03

Integrál

#2 20. 04. 2013 10:21 — Editoval found (20. 04. 2013 10:23)

Re: Integrál

#3 20. 04. 2013 10:34

Re: Integrál

#4 20. 04. 2013 10:42

Re: Integrál

#5 20. 04. 2013 11:08 — Editoval found (20. 04. 2013 11:12)

Re: Integrál

#6 21. 04. 2013 02:57

Re: Integrál

Zápatí