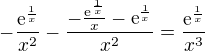Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 04. 2013 00:14
- maroslav91

- Zelenáč
- Příspěvky: 3
- Škola: VŠB-TUO
- Pozice: student
- Reputace: 0
Derivace funkce
Zdravím všechny
Potřeboval bych pomoct s druhou derivací y=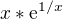
první derivace mi vyšla y´=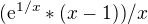 a myslím si že by měla být dobře, ale nevím jak z toho vypočíst druhou, díky za pomoc
a myslím si že by měla být dobře, ale nevím jak z toho vypočíst druhou, díky za pomoc
Offline
- (téma jako vyřešené označil(a) maroslav91)
#2 21. 04. 2013 01:08
- 010010

- Příspěvky: 82
Re: Derivace funkce
Áno, prvá je dobre.
Roznásob zátvorku a použi deriváciu podielu. S deriváciou súčinu zrejme problém nemáš.
Offline
#3 21. 04. 2013 09:04
- maroslav91

- Zelenáč
- Příspěvky: 3
- Škola: VŠB-TUO
- Pozice: student
- Reputace: 0
Re: Derivace funkce
↑ 010010:
Když to roznásobím, mám potom derivovat podle vzorce (u/v)' ? a "u" brát jako 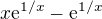 ?
?
Offline
#5 21. 04. 2013 13:13
- maroslav91

- Zelenáč
- Příspěvky: 3
- Škola: VŠB-TUO
- Pozice: student
- Reputace: 0
Re: Derivace funkce
↑ jarrro:
to by mě nenapadlo, děkuji :-)
Offline