Matematické Fórum

bejf · 21. 04. 2013 21:38 — Editoval bejf (21. 04. 2013 21:44)

Ahoj. Mám problém s důkazem jedné posloupnosti, že je rostoucí.
$$\frac{2n+1}{n+2}$^\infty_{n=1}$

Vzal jsem tedy $a_{n}=\frac{2n+1}{n+2}$ a $a_{n+1}=\frac{2n+2}{n+3}$ .

Z definice posloupnosti plyne, že je rostoucí, právě když: Je-li $r<s$ pak $a_{r}<a_{s}$ .

Nuže opravdu platí $a_{n}<a_{n+1}$ , potom by mělo platit také pro všechna 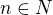$n\in N$ nerovnost
$\frac{2n+1}{n+2}<\frac{2n+2}{n+3}$ (násobím kladnými čísly)
$(2n+1)(n+3)<(2n+2)(n+2)$
$2n^2+7n+3<2n^2+6n+4$

Poslední nerovnost ale už nějak neplatí. Takže toť můj postup, ve kterém asi dělám chybu nebo na něco zapomínám. Děkuji za rady.