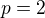Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 22. 04. 2013 19:11 — Editoval bonifax (22. 04. 2013 19:20)
Re: kuželosečky
↑ Adulka:
Ahoj,
ve 4.řádku je chyba, ale 5. je zas dobře, takže asi překlep.
Ne, z toho vyplývá parabola bude otočené směrem doprava tedy takto 
Parametr je správně.
Ohnisko bude ležet napravo od vrcholu a vzdálenost mezi ohniskem a vrcholem je p/2. Ypsilonová souřadnice ohniska bude stejná jako u vrcholu a x-ova bude posunuta o p/2 od vrcholu.
Přímka d je řídící přímka. V našem případě bude procházet nějakým bodem na ose x nalevo od vrcholu. Tedy rovnice bude ve tvaru x=.....
Vypočítame ji, tak, že od x-ove souradnice stredu odecteme p/2.
Offline
#3 22. 04. 2013 19:16
Re: kuželosečky
↑ bonifax:
rovnici řídící přímky nepotrebuji jen ji zamalovat takze od vrchollu dam do leva 1??
a to ohnisko tedy bude ![kopírovat do textarea $F[4;2]$](/mathtex/24/2418e8408f75e8a9bc586b95b75e92f3.gif) ??
??
Offline
#4 22. 04. 2013 19:18 — Editoval bonifax (22. 04. 2013 19:23)
Re: kuželosečky
↑ Adulka:
Ano:-)
Ano:)
EDIT..
promiň přepsal jsem se v předchozím příspěvku.
Řídící přímka bude NALEVO od vrcholu jako tady
Offline
#5 22. 04. 2013 19:33
Re: kuželosečky
↑ bonifax:
a nevis jeste tu jednu kuzelosecku jak tu mam danou vychazi tam hnusny cisla..
Offline







![kopírovat do textarea $V[3;2]$](/mathtex/cf/cf77750120f5667b45e0c4c92135665f.gif)