Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Zbytek 2^Fibonacci(n) po dělení prvočíslem (TOTO TÉMA JE VYŘEŠENÉ)
#1 22. 04. 2013 00:29 — Editoval Pavel Brožek (22. 04. 2013 00:41)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Zbytek 2^Fibonacci(n) po dělení prvočíslem
Jak byste spočítali
kde  je prvočíslo a n přirozené číslo?
je prvočíslo a n přirozené číslo? 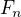 značí n-té Fibonacciho číslo. Zajímal by mě nějaký efektivní algoritmus, který by spočítal výsledek v rozumném čase i pro hodnoty asi
značí n-té Fibonacciho číslo. Zajímal by mě nějaký efektivní algoritmus, který by spočítal výsledek v rozumném čase i pro hodnoty asi  a
a  , např.
, např.  a
a  .
.
Offline
- (téma jako vyřešené označil(a) Pavel Brožek)
#2 22. 04. 2013 19:45 Příspěvek uživatele OiBobik byl skryt uživatelem OiBobik.
#3 22. 04. 2013 20:22 — Editoval Pavel Brožek (22. 04. 2013 20:25)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zbytek 2^Fibonacci(n) po dělení prvočíslem
↑ OiBobik:
Ahoj,
1) no řekněme, že budeme mít počítač, který vykoná  operací za vteřinu (podle toho, co jsem teď našel na googlu, tak by to měl být zhruba lepší stolní počítač, řádově to snad bude odpovídat). Dejme tomu, že chci, abych výsledek měl do minuty. Takže jsem shora omezený asi
operací za vteřinu (podle toho, co jsem teď našel na googlu, tak by to měl být zhruba lepší stolní počítač, řádově to snad bude odpovídat). Dejme tomu, že chci, abych výsledek měl do minuty. Takže jsem shora omezený asi  operacemi.
operacemi.  , takže to už je moc. A to těch
, takže to už je moc. A to těch  operací za vteřinu je asi hodně optimistické, budou to nejspíš instrukce procesoru, operace v téhle úloze bude zahrnovat možná tisíce (úplně hádám) instrukcí procesoru.
operací za vteřinu je asi hodně optimistické, budou to nejspíš instrukce procesoru, operace v téhle úloze bude zahrnovat možná tisíce (úplně hádám) instrukcí procesoru.
2) Jak to přesně myslíš? Číslo 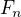 vůbec nemůžu spočítat, je strašně obrovské (Přibližně
vůbec nemůžu spočítat, je strašně obrovské (Přibližně  ,
,  je zlatý řez), řádově má teda asi
je zlatý řez), řádově má teda asi  míst, pokud mám RAM
míst, pokud mám RAM  , tak by ani nebylo kam uložit. Bude to chtít nějaký trik, pokud to vůbec půjde.
, tak by ani nebylo kam uložit. Bude to chtít nějaký trik, pokud to vůbec půjde.
Edit: Vidím, že jsi svůj příspěvek skryl, snad můj příspěvek i tak dává smysl, tak ho tu už nechám.
Offline
#4 22. 04. 2013 21:57 — Editoval OiBobik (22. 04. 2013 22:07)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Zbytek 2^Fibonacci(n) po dělení prvočíslem
↑ Pavel Brožek:
Tak ja napisu naznak toho, jak jsem uvazoval (neni to nic svetobornyho, spis takovy odrazovy mustek, ktery by snad mohl jit nejak vylepsit)
1. Nejprve zkusme zjistit, jak prijit na Fn modulo d, kde d je nejake prir. Cislo:
budu uvazovat dvijice po sobe jdoucich fib cisel modulo d, znacit to budu (A_k,B_k); zrejme pak plati (A_(k+1),B_(k+1))=(B_k,A_k+B_k mod d).
Ted: vsech moznych takovych dvojic je nejvyse d^2 a plati, ze kazda dvojice jednoznacne urcuje tu nasledujici. Tedy po nejvyse d^2 krocich se (teoreticky) vypocet zacykli a pak se opakuje periodicky nejaka posloupnost dvojic. Kdybychom znali delku pocatecniho useku ("pred prvni periodou"), ozn. P, a delku periody L, pak spocitame (A_n,B_n) jako (A_(n-P mod L), B_(n-P mod L)). Pritom dostat se ke dvojici takoveho indexu uz stoji "jen" (radove) L operaci, pritom L<d^2.
(Na tuto cast smerovaly oba dotazy - z druhe casti poplyne, ze by se hodilo d=p-1, a taky moci kodulit cislo n cislem L .. nikoli tedy cislo Fn, jen ten index)
No a druha vec je, ze pro x nesoudelne s p prvocislem plati x^(p-1) mod p =1 - tedy spec. Pro tvuj priklad je 2^(Fn) mod p =2^(Fn mod (p-1)) mod p. To jsou obecne vzato sice porad velka cisla, ale uz to nejsou aspon tak obludne velka cisla, ze by nevlezla do pameti apod.
Pozn: prinejmensim ta prvni cast bude urcite nejak vylepsit - bud dobrym odhadem (ktere dvojice muzou byt zmodulena dve po sobe jdouci fib cisla?) Nebo nejakym odvozenim explicitni formule fib cisla "modulo d".
Taky se omlouvam za neladnou formu, skrabu to na mobilu.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 22. 04. 2013 23:14 — Editoval Pavel Brožek (22. 04. 2013 23:14)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zbytek 2^Fibonacci(n) po dělení prvočíslem
↑ OiBobik:
Díky, tvá odpověď mě přivedla k novým myšlenkám. Přečetl jsem si konečně podrobněji článek na wikipedii o periodě Fibonacciho posloupnosi modulo nějaké číslo. Je zajímavé, že pokud by číslo 5 bylo čtvercem  a číslo 2 by mělo inverzi
a číslo 2 by mělo inverzi  (což je pro prvočíslné p zásadní problém :D), pak se dá zlatý řez zapsat jako
(což je pro prvočíslné p zásadní problém :D), pak se dá zlatý řez zapsat jako  a n-té Fibonacciho číslo (z explicitního vyjádření n-tého členu pomocí zlatého řezu) jako
a n-té Fibonacciho číslo (z explicitního vyjádření n-tého členu pomocí zlatého řezu) jako
což je už pěkné a problém by to vyřešilo (jestli se nepletu). Bohužel to pro prvočíselná  vůbec nefunguje a nenapadá mě, jestli by se idea toho postupu dala využít i na prvočíselná p a taková p, kde 5 nebude mít odmocninu.
vůbec nefunguje a nenapadá mě, jestli by se idea toho postupu dala využít i na prvočíselná p a taková p, kde 5 nebude mít odmocninu.
Offline
#6 22. 04. 2013 23:26 — Editoval Pavel Brožek (22. 04. 2013 23:39)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zbytek 2^Fibonacci(n) po dělení prvočíslem
Tak jestli jsem něco nepřehlídl, tak už asi máme efektivní řešení. Jak jsi navrhl, tak z Malé Frematovy věty máme
Jakmile zjistíme exponent, tak už je jednoduché dopočítat zbytek. už snadno spočítáme v rozumném čase pomocí postupu uvedeného tady (využívá toho, že
už snadno spočítáme v rozumném čase pomocí postupu uvedeného tady (využívá toho, že 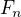 je prvek jedné matice umocněné na n-tou, stačí tu matici mocnit modulo
je prvek jedné matice umocněné na n-tou, stačí tu matici mocnit modulo 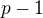 ). Počet mocnění bude zhruba
). Počet mocnění bude zhruba  , takže počet operací by měl být na běžném počítači snadno zvladatelný.
, takže počet operací by měl být na běžném počítači snadno zvladatelný.
Offline
#7 22. 04. 2013 23:43
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Zbytek 2^Fibonacci(n) po dělení prvočíslem
↑ Pavel Brožek:
Supr.
Tak jenom poznamka: odhad uvedeny zde, 1. Odkaz, strana asi 26, uvadi, ze p(n)<=6n, kde p(n) je ta Pisanova perioda modulo n. Z toho plyne?, ze i ten muj naivni algoritmus by mel casovou narocnost "jen" O(p).
A jeste dotaz: je to k necemu dobre? :) prijde mi, ze te takovy priklad asi nenapadl jen tak. Na druhou stranu, netusim, kde by se takovy problem vyskytl prirozene.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#8 22. 04. 2013 23:53 — Editoval Pavel Brožek (22. 04. 2013 23:53)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zbytek 2^Fibonacci(n) po dělení prvočíslem
↑ OiBobik:
Jedna úloha z http://projecteuler.net/ vede právě na vyčíslování podobných výrazů. Bylo na tom hodně jiné práce než se člověk dostal k tomuhle, takže když vidíš to zadání, tak bys asi nejdřív vůbec netipnul, že to povede na takové věci :). Je to hrozně zajímavá úloha, bavilo mě ji řešit. Teď už mi zbývá jen implementovat ten algoritmus :)
Offline
#9 23. 04. 2013 18:49
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Zbytek 2^Fibonacci(n) po dělení prvočíslem
↑ Pavel Brožek:
Desim se pomyslet, jakym zpusobem to na to vede : )) pekne.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#10 23. 04. 2013 20:23
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Zbytek 2^Fibonacci(n) po dělení prvočíslem
Ahoj,
téma čtu až teď. Napadly mě dvě věci, ale asi budou časově náročnější. Vycházím z odkazu na wikipedii.
1)  spočítat na základě dvou rekurentních vztahů v této kapitole zcela na jejím konci - časová složitost je O((log(n)) a v každém kroku bychom prováděli mod p-1.
spočítat na základě dvou rekurentních vztahů v této kapitole zcela na jejím konci - časová složitost je O((log(n)) a v každém kroku bychom prováděli mod p-1.
2) Zvládneme-li faktorizaci p-1 na prvočísla, mohli bychom využít toto - a zkoumat  pro q prvočíslo a využít předchozí odkaz a následně např. pomocí čínské zbytkové věty získat výsledek. To nám asi pomůže jen velmi málo - musíme se snažit při rekurentních vztazích získat
pro q prvočíslo a využít předchozí odkaz a následně např. pomocí čínské zbytkové věty získat výsledek. To nám asi pomůže jen velmi málo - musíme se snažit při rekurentních vztazích získat 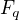 .
.
Časové složitosti jsem detailně nepropočítával, ale asi to nebude nic moc.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Zbytek 2^Fibonacci(n) po dělení prvočíslem (TOTO TÉMA JE VYŘEŠENÉ)