Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 04. 2013 12:14 — Editoval denier (28. 04. 2013 12:15)
Základní poznatky
3 dny před maturitou zjišťuji, že nemám jasno v úplně elementárních věcech.. tak např.
Absolutní hodnota ze záporného čísla je číslo kladné, z kladného taky kladné, prostě je to vzdálenost od 0.
V článku o abs.h. na matwebu ale čtu Budeme-li ovšem chtít zjistit absolutní hodnotu ze záporného čísla, bude to číslo opačné (tedy z x, kde x < 0 bude absolutní hodnota −x
Jak může být absolutní hodnota -x? Ze záporného je to přece číslo opačné, tzn +x?
A dálší případ
mám rovnici 
upravím ji na 
a umocním ji na druhou 
když jsem to počítal sám tak jsem dával  do absolutní hodnoty, protože po umocnění odmocniny má přece vyjít absolutní hodnota daného čísla.. jakto, že to tak není v tomto příkladu?
do absolutní hodnoty, protože po umocnění odmocniny má přece vyjít absolutní hodnota daného čísla.. jakto, že to tak není v tomto příkladu?
Offline
- (téma jako vyřešené označil(a) denier)
#3 28. 04. 2013 12:29 — Editoval marnes (28. 04. 2013 12:30)
- marnes

- Příspěvky: 11227
Re: Základní poznatky
↑ denier:
Správně píšeš, že AH ze záporného je číslo kladné. Ale toto číslo kladné vytvoříš jako číslo opačné k zápornému
pro druhý dotaz odpovím tak, že umocnění není ekvivalentní úprava a pak je potřeba zkoušky a do AH bych dával výraz, pokud bych odmocńoval např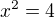
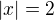
Jo. A na začátku vás zdravím.
Offline
 nějaké číslo z intervalu
nějaké číslo z intervalu 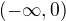 a dostaneš třeba pro
a dostaneš třeba pro 
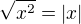 zde odmocňuješ
zde odmocňuješ zde umocňuješ
zde umocňuješ