Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergence řady se sinem (TOTO TÉMA JE VYŘEŠENÉ)
#2 28. 04. 2013 22:18
Re: Konvergence řady se sinem
Dobrý den
Pokud zadání vyžaduje určit pouze bodovou konvergenci (pro která x je řada konvergentní), tak napřed zkus určit, pro která x je splněna nutná podmínka konvergence (limita posloupnosti rovna 0), a pakliže je splněna tak si stačí uvědomit že posloupnost je alternující a dál už by neměl být žádný problém.
Offline
#3 28. 04. 2013 22:54
Re: Konvergence řady se sinem
↑ Brzls:
Tak jsem si ten výraz bez té -1 upravil a hledal, kdy 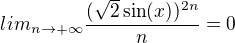 . Pak jsme si řekl, že to nastane, když bude
. Pak jsme si řekl, že to nastane, když bude a z toho už x dokážu dostat. Jen je to spíš takový odhad a nevím, jak to podložit exaktně. Taky nevím, jestli neexistují i jiná x, pro která by limita vyšla 0. Každopádně dále by Leibnizovo kritérium rozhodlo o konvergenci řady.
a z toho už x dokážu dostat. Jen je to spíš takový odhad a nevím, jak to podložit exaktně. Taky nevím, jestli neexistují i jiná x, pro která by limita vyšla 0. Každopádně dále by Leibnizovo kritérium rozhodlo o konvergenci řady.
Ale jak je to s konvergencí absolutní a neabsolutní?
Offline
#4 28. 04. 2013 23:42
Re: Konvergence řady se sinem
To co si napsal je správně (a podle mě to i exktní je). Co se týče absolutní konvergence, tak je potřeba určit jestli konverguje právě ten výraz bez (-1)na n. Na to je podle mě ideální odmocninové kritérium, pomocí kterého ukážu pro která je to konvergentní absolutně (je třeba si dát pozor na případ když se potom ta limita bude rovna 1 a tuto možnost vyšetřit zvlášť). No a co se týká stejnoměrné konvergence (pakliže řadu vnímám jako řadu funkcí) tak přiznávám že mě nic nenapadá.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergence řady se sinem (TOTO TÉMA JE VYŘEŠENÉ)

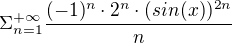 .
.