Matematické Fórum

FrantisekSW · 01. 05. 2013 16:59

Dobrý den, potřeboval bych pomoct s výpočtem těch příkladů na téma kružnice, byl bych Vám moc vděčný za každou pomoc, nejlépe za vypočtení celého příkladu, jelikož jsem se s tím setkal poprvé, takže v tom mám trochu větší zmatek.

P.S byl bych rád kdyby mi šlo pomoct ještě dnes, mockrát děkuji.

souteh · 01. 05. 2013 17:04

Doplnění na čtverec ti něco říká nebo je nutné vysvětlit?

P.S: Pro každý příklad doporučuji vlastní vlákno, ať se to tu pak nemotá.

FrantisekSW · 01. 05. 2013 17:07

↑ souteh:

Omlouvám se ale moc neříká, jsem ze školy už nějakou dobu, takže je to se mnou tak trochu těžké, rád s Vámi budu spolupracovat , ale asi by bylo lehčí kdyby jste mi to ukázal celé.

souteh · 01. 05. 2013 17:20 — Editoval souteh (01. 05. 2013 17:29)

Základ je znát obecnou rovnici kružnice, ta je: $(x-x_{s})^{2}+(y-y_{s})^{2}=r^{2}$ ..

$x_{s}$ je x-ová souřadnice středu kružnice,
$y_{s}$ je y-ová souřadnice středu kružnice,
$r$ je poloměr kružnice.

Rovnici lze vydělit 5, dostaneme: $x^{2}+y^{2}-6x+4y=0$ .

Nyní chceme tuto rovnici dostat ve středovém tvaru, dáme k sobě $x$ a $y$ :

$x^{2}-6x+y^{2}+4y=0$

Tuto rovnici potřebujeme dostat do základní rovnice kružnice (viz výše), provedeme právě doplnění na čtverec, kterým dostaneme 2 závorky umocněné na druhou.

z $x^{2}-6x$ dostaneme $(x-3)^{2}$ , protože platí $(a-b)^{2}=a^{2}-2ab+b^{2}$ .

To není všechno... je nutné uvědomit si, že po roznásobení dostaneme $x^{2}-6x+9$ , a proto musíme tu devítku následně odečíst.

Bude tedy: $(x-3)^{2}-9$

Úplně stejným způsobem uděláme $y$ . Dostaneme $(y+2)^{2}-4$

Pak už jen složíme dohromady:

$(x-3)^{2}-9+(y+2)^{2}-4=0$
$(x-3)^{2}+(y+2)^{2}=13$ .. to už je obecný tvar kružnice, jak jsem psal na začátku, z něj snadno vidíme, že:

$S[3;-2]$ a $r=\sqrt{13}$

hradecek

↑ FrantisekSW:
Priesečníky dostaneš \jednudocho, tak že vieš, že pre nejaký bod(y) musia platiť obe rovnice...
Pretože priesečník leží ako na priamke tak aj na kružnici...takže keď ho dosadíš do oboch rovníc musia obidve platiť....
Teda riešiš sústavu dvoch rovníc o dvoch neznámych...

$x-2y+5=0\\ x^2+y^2=25$

Z prvej vyjadrím $x$ a dosadím do druhej...
$(2y-5)^2+y^2=25$
upravím, dostanem kvadratickú rovnicu...t.j. dva 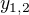$y_{1,2}$ a ku každému zvlášť dopočítam $x_1$ a $x_2$
Dostal som teda dva body, pre ktoré sú splné obe rovnice a to sú hľadané priesečníky $P_1=[x_1;y_1]$ a $P_2=[x_2;y_2]$

Matematické Fórum

#1 01. 05. 2013 16:59

Kružnice

#2 01. 05. 2013 17:04

Re: Kružnice

#3 01. 05. 2013 17:07

Re: Kružnice

#4 01. 05. 2013 17:20 — Editoval souteh (01. 05. 2013 17:29)

Re: Kružnice

#5 01. 05. 2013 17:49 — Editoval hradecek (01. 05. 2013 17:56)

Re: Kružnice

Zápatí