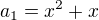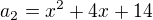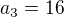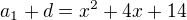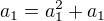Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 01. 05. 2013 19:23
Re: Aritmetická posloupnost
↑ wolfito:
Předem říkám, že jsem to nepočítal, ale
a1+d=a2
a2+d=a3
Když dosadíš za a1,a2,a3, dostaneš dvě rovnice pro dvě neznámé x a d.
Offline
#4 01. 05. 2013 19:34
Re: Aritmetická posloupnost
↑ wolfito:
Ano, ale  i
i 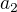 máš v zadání jako funkce x, tak je tam dosaď. Pak už to půjde dobře, nejlépe z jedné rovnice vyjádřit d (které tě stejně moc nezajímá) a dosadit do druhé.
máš v zadání jako funkce x, tak je tam dosaď. Pak už to půjde dobře, nejlépe z jedné rovnice vyjádřit d (které tě stejně moc nezajímá) a dosadit do druhé.
Tentokrát jsem si to radši spočítal, vede to na kvadratickou rovnici, vychází to hezky, řešení jsou dokonce dvě.
Offline

 tak, aby čísla
tak, aby čísla 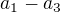 tvořila tři následující členy AP:
tvořila tři následující členy AP: