Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 02. 05. 2013 13:01
Re: Monožina v C
↑ Simon P40:čo je to identický? úplne rovnaký samozrejme nie je v reálnych číslach je to interval a v komplexných medzikružie
MATH IS THE BEST!!!
Offline
#7 02. 05. 2013 18:30
Re: Monožina v C
↑ Simon P40:
Jen bych dodal, že komplexní čísla nacházející se na kraji menší kružnice patří do mezikruží, ovšem komplexní čísla na okraji větší kružnice už ne. Viz znaménka nerovností v zadání.
Offline

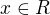 na ose...
na ose... je roven vzdálenosti bodu
je roven vzdálenosti bodu  od bodu
od bodu  , pří čemž tato vzdálenost bodů Gaussovy roviny
, pří čemž tato vzdálenost bodů Gaussovy roviny ?
?
