Matematické Fórum

steeldog · 02. 05. 2013 17:37

Prosil bych o pomoc s:

Jakou podmínku musí splňovat střed S[m;n] kružnice s poloměrem r=3, aby se kružnice dotýkala přímek, které mají rovnice y = 2x a y = (1/2)x?

Díky moc

hradecek · 02. 05. 2013 19:43

↑ steeldog:
Kružnica musí mať s priamkami práve jeden spoločný bod...

Jj · 02. 05. 2013 19:50 — Editoval Jj (02. 05. 2013 20:01)

↑ steeldog:
Střed leží ve vzdálenosti r od každé z přímek.
Čili dvě rovnice s absolutními hodnotami pro m, n. Z názoru vyplývá, že by měly mít 4 řešení.

steeldog · 02. 05. 2013 22:07

↑ Jj:

podle učebnice je výsledek (2m-n)^2=45 a (2n-m)^2=45, takze m=n=+-3(5)^(1/2) nebo m=-n=-+(5)^(1/2)

zajímalo by mě prosím jak na to přijít

zdenek1 · 03. 05. 2013 07:35

↑ steeldog:
$p:y=2x\ \Rightarrow\ p:2x-y=0$
$q:y=\frac x2\ \Rightarrow\ x-2y=0$

vzdálenost středu od přímky $p$ : $d(S,p)=\frac{|2m-n|}{\sqrt5}=3\ \Rightarrow\ |2m-n|=3\sqrt5$ umocnit
vzdálenost středu od přímky $q$ : $d(S,q)=\frac{|m-2n|}{\sqrt5}=3\ \Rightarrow\ |m-2n|=3\sqrt5$ umocnit

Cheop · 03. 05. 2013 07:51

↑ steeldog:
Podle mě budou řešení 4
Střed bude ležet na ose úhlu těch 2 přímek tedy na přímce 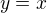$y=x$
nebo na její kolmici tj na přímce 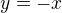$y=-x$
Tedy střed bude mít souřadnice:
$S_1=(m;\,m)\\S_2=(-m;\,-m)\\S_3=(-m;\,m)\\S_4=(m;\,-m)$
A pak dostaneme:
1)
$\frac{|2m-m|}{\sqrt 5}=3$
2)
$\frac{|2m+m|}{\sqrt 5}=3$