Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » minimální polynom inverzního prvku (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 05. 2013 17:52
minimální polynom inverzního prvku
Ahoj,
potřebovala bych pomoct s tímto příkladem:
Buď  rozšíření těles a
rozšíření těles a  . Vyjádřete polynom
. Vyjádřete polynom 
pomocí koeficientů polynomu  .
.
Nevím moc, jak na to jít. Zkoušela jsem to na pár příkladech a vidím tam nějaké shodné znaky, ale nevím, jak to odvodit obecně.
příklad 1![kopírovat do textarea $\alpha = \sqrt[3]{1 + \sqrt{2}} - \frac{1}{\sqrt[3]{1 + \sqrt{2}}}\\
m_{\alpha,\mathbb{Q}} = x^3 + 3x -2\\
m_{\alpha^{-1},\mathbb{Q}} = x^3 - \frac{3}{2}x^2 -\frac{1}{2}$](/mathtex/1e/1e6ccf989286135e5198ba3bb401880d.gif)
příklad 2
Jde vidět, že poslední člen je inverzní a potom mám pocit, že poslední člen vydělí ostatní, ale u příkladu 1 se prohazují členy.. Nevíte někdo prosím, jak na to?
Offline
- (téma jako vyřešené označil(a) drabi)
#3 05. 05. 2013 18:38
Re: minimální polynom inverzního prvku
↑ jarrro:
Ahoj, díky za reakci. Už to vidím, akorát si nejsem jistá, zda je úplně zřejmé, že se jedná o minimální polynom toho inverzního prvku, jestli bys mi mohl ukázat, jak to z toho plyne? Díky
Offline
#4 05. 05. 2013 18:46 — Editoval OiBobik (05. 05. 2013 18:47)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: minimální polynom inverzního prvku
↑ drabi:
Čau,
pozorování 1:  . Spec. tedy ty minimální polynomy mají stejný stupeň (Zkus to nahlédnout/dokázat).
. Spec. tedy ty minimální polynomy mají stejný stupeň (Zkus to nahlédnout/dokázat).
Tedy stačí zkrátka najít nějaký polynom, jehož kořenem je 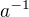 a je stupně stejného, jako
a je stupně stejného, jako  .
.
Takže označme  (búno jej bereme monický).
(búno jej bereme monický).
Máme tedy 
Zkus to upravit do tvaru, kde vystupují koeficienty  a výrazy
a výrazy 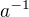 .
.
Edit: Vidím, že píšu pozdě, ale nechám to už tady (částečně to odpovídá na druhý dotaz).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 05. 05. 2013 18:47
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » minimální polynom inverzního prvku (TOTO TÉMA JE VYŘEŠENÉ)

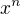 z toho to už priamo vidno
z toho to už priamo vidno