Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 06. 01. 2009 15:48 — Editoval lukaszh (06. 01. 2009 15:53)
Re: Kombinace
↑ Lucas456:
Neviem presne čo potrebuješ, ale pravdepodobne zistiť triedu kombinácii: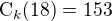
Pre kombinácie platí:
A tento vzorec aplikuješ na svoj príklad:
Porovnávaním čitateľov odhadnem:
Toto m dosadím do menovateľa:
Porovnám a dostanem: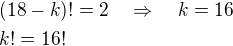
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#4 06. 01. 2009 20:01
#5 06. 01. 2009 20:54
Re: Kombinace
↑ Chrpa: ↑ Lucas456:
A po tretie sú to kombinácie 16 triedy z 18 prvkov :-)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#8 08. 01. 2009 15:55
Re: Kombinace
a čo tak opačný postup ?,vo vzorci MUSÍ existovať nejaký vzťah medzi premennými...
Matematiku nemám rád - je to veda o nekonečnom,narozdiel od fyziky - fyzika je len taká veľká ako priestor...moje myslenie...
Najkratšie odpovede – áno a nie – vyžadujú najdlhšie rozmýšľanie.Pythagoras
Offline
#9 08. 01. 2009 16:26 — Editoval O.o (08. 01. 2009 16:27)
Re: Kombinace
↑ Lucas456:
Ahoj .),
původně jsi nezapsal přesné zadání, asi jsi málo upozorňoval na přepsání .)
U kombinací půjde o kombinační číslo, proto doporučuji mrknout, alespoň na výpočet čísla , např. matweb (patří k němu toto forum, tak určitě najdeš sám) nebowiki.
Změním tvoji neznámou z x na n (odkaz na wiki používá jako počet prvků n, tak abys to lépe viděl), krom toho jednou píšeš x a jednou n, tak se nedivím, že občas někdo enví, co přesně potřebuješ .)
Lepší?
Offline
#11 08. 01. 2009 20:21
Re: Kombinace
↑ Lucas456:
Jestli je x jedna neznámá a vyjadřuje jednu stejnou záležitost, tak to můžeš rpavděpodobně řešit obdobně. Jestli je troska ten, který něco nedokáže zrovna náhodou vyřešit, pak bych hádal, že svět je takových trosek plný .).
PS Určitě ti tu všichni fandí, když ses dal an učení matematiky, za to palec nahoru ;)
Offline
