Matematické Fórum

↑ mp3jj:

zdravím :-)

obdobně, jako jsi napsal součiny 1) = 2) zapíšeš součiny pro :

1) = 3)

2) = 3)

je dobre si všimnout, že 84.32.a=84.144.b levou a právou stránu lze vydělit největším společným dělitelem. Stejně to bude i pro další rovnice.

OK?

↑ mp3jj:[[img][/img]  vycházim z toho,že a=4,5b ,tak pak ti zbydou 2 soustavy rovnic.  84*32*a= a*b*c
                                                                                                                                                            84*144*b=a*b*c
a z toho by mělo jít odvodit,že a=144 ,b = 32 ,c= 84 nebo ,ne? :-)

Z 1. a 2. řádku mám rovnost
Jestliže se bavíme o přirozených číslech, pak nejmenší a je 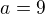, pak a z toho - to je tedy mejvětší c.

Pokud předpokládám, že nejmenší c by mohlo být 1, musím najít a a b,aby to platili.

Pokud c=1, tak potom 84*32*a=84*144*b=a*b - ale to je přeci snadné
potom a=84*144=12 096
b=84*32=2688

Pokud by to mohlo být třeba reálné číslo, troufnu si říct, že c by mohlo být jakékoliv.
Pokud by šlo o celá čísla, tak by nejmenší a mohlo být i -9, pak by b bylo -2. c by pak bylo také záporné, protože 1. by byla záporná, 2. také a ve 3.je ab, což by dalo +, proto by c muselo být záporné, aby 3.byla také záporná.

Do komplexních čísel se radši pouštět nebudem.