Matematické Fórum

Maros · 05. 05. 2013 12:53

Zdravím chcel by som si overiť, či je tento vzťah správny . Vozidlo s čelnou plochou $S_{x}$ , koeficientom odporu vzduchu $c_{x}$ sa pohybuje konštantnou rýchlosťou "v" vo vzduchu o hustote $\varrho$ . Začne spomaľovať konštantným zrýchlením "a" až zastane. Energia potrebná na prekonanie odporu vzduchu: $E=\frac{1}{4} \cdot c_{x} \cdot S_{x}\cdot \frac{\varrho }{2}\cdot \frac{v^{4}}{a}$

GeekRobert · 06. 05. 2013 18:15

Ak spomaľuje konštantne tak mi to vychádza $E = \frac{1}{4} * c_{x} * S_{x} * \varrho * \frac{v^{4}}{a}$ .
Odkiaľ si dostal $\frac{\varrho }{2}$ ??

Maros · 07. 05. 2013 11:01 — Editoval Maros (07. 05. 2013 11:05)

$\frac{\varrho }{2}$ je zo základného vztahu pre odpor vzduchu $O_{vz}=\frac{1}{2}S_{x}\cdot c_{x}\cdot \varrho _{vz}\cdot v^{2}$ , ktorý sa dosadí do vztahu pre energiu $E=\int_{0}^{t_{a}}F_{vz}\cdot v dt = \int_{0}^{t_{a}}\frac{1}{2}S_{x}\cdot c_{x}\cdot \varrho _{vz}\cdot v^{2}\cdot v dt =\frac{1}{2}S_{x}\cdot c_{x}\cdot \varrho _{vz}\int_{0}^{t_{a}} v^{3}dt$ a $v$ sa da vyjadrit ako $a\cdot t$ dosadi sa $E=\frac{1}{2}S_{x}\cdot c_{x}\cdot \varrho _{vz}\int_{0}^{t_{a}} (a\cdot t)^{3}dt =\frac{1}{2}S_{x}\cdot c_{x}\cdot \varrho _{vz}\cdot a^{3}[\frac{( t)^{4}}{4}]^{ta}_{0}=\frac{1}{2}S_{x}\cdot c_{x}\cdot \varrho _{vz}\cdot a^{3}\cdot \frac{ t_{a}^{4}}{4}$ a $t_{a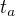}$ je čas zastavenia a to je $t_{a}=\frac{v}{a}$ vysledný vztah po vykratení $a$ je $E=\frac{1}{4} \cdot c_{x} \cdot S_{x}\cdot \frac{\varrho }{2}\cdot \frac{v^{4}}{a}$ toto odvodenie som nasiel v jednej práci a vyzerá to dobre preto zistujem ci je niekde chyba.

GeekRobert · 07. 05. 2013 18:20

Ak to počítaš cez integrály tak spočítaš aj so skutočným spomaľovaním (v skutočnom svete), ktoré konštantné není. Pretože pri nižšej rýchlosti sa zníži odpor vzduchu a aj spomaľovanie. Môj vzorec ráta s konštantným spomaľovaním.
V tvojom zápise som nenašiel chybu. Podľa mňa to máš správne.

Matematické Fórum

#1 05. 05. 2013 12:53

Energia potrebna na prekonanie odporu vzduchu

#2 06. 05. 2013 18:15

Re: Energia potrebna na prekonanie odporu vzduchu

#3 07. 05. 2013 11:01 — Editoval Maros (07. 05. 2013 11:05)

Re: Energia potrebna na prekonanie odporu vzduchu

#4 07. 05. 2013 18:20

Re: Energia potrebna na prekonanie odporu vzduchu

Zápatí