Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 05. 2013 22:19 — Editoval jendula11 (09. 05. 2013 22:20)
obsah plochy
Pěkný večer, moc bych prosil o radu jak spočíst následující příklad:
Vypočtete obsah obrazce, ohraničeného křivkami: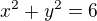 a
a 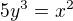 y>0
y>0
Vyjádřil bych si z každé rovnice y: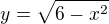 a
a ![kopírovat do textarea $y=\sqrt[3]{\frac{x^{2}}{5}}$](/mathtex/33/3343d39baa809a3bcbf0d609712bbeae.gif)
Akorát nevím jak na integrační meze a jak si sestavit daný integrál.
Velmi děkuji za pomoc.
Offline
#2 09. 05. 2013 22:45 — Editoval dugbutabi (10. 05. 2013 11:50) Příspěvek uživatele dugbutabi byl skryt uživatelem dugbutabi.
#3 09. 05. 2013 22:55 — Editoval jendula11 (09. 05. 2013 22:55)
Re: obsah plochy
↑ dugbutabi:
Dobře, díky za radu. Rozumím tedy tomu správně, že by integrál měl vypadat takto:![kopírovat do textarea $S=\int_{-\sqrt{5}}^{\sqrt{5}}\sqrt{6-x^{2}}-\sqrt[3]{\frac{x^{2}}{5}}dx$](/mathtex/02/022806f158ec95d808db6b639418b201.gif)
Děkuji
Offline
#4 09. 05. 2013 22:57 Příspěvek uživatele dugbutabi byl skryt uživatelem dugbutabi.
#5 09. 05. 2013 23:02 — Editoval dugbutabi (09. 05. 2013 23:03) Příspěvek uživatele dugbutabi byl skryt uživatelem dugbutabi.
#6 09. 05. 2013 23:31
Re: obsah plochy
↑ dugbutabi:
No výsledky k tomu nemám. Jen mě zajímalo jestli mám správně sestavenou formulaci toho integrálu. Samotný výpočet už mi problémy nedělá.
Díky
Offline
#7 09. 05. 2013 23:50 — Editoval dugbutabi (09. 05. 2013 23:51) Příspěvek uživatele dugbutabi byl skryt uživatelem dugbutabi.
#8 10. 05. 2013 00:10 — Editoval dugbutabi (10. 05. 2013 00:11) Příspěvek uživatele dugbutabi byl skryt uživatelem dugbutabi.
#9 10. 05. 2013 11:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: obsah plochy
↑ jendula11:
Zdravím,
nevím, jak vidí kolegové, ale mně se zda zadání nepřesné, jelikož dle zadání stejně dobře mohu počítat obsah plochy nebo obsah plochy. Nebo také stejně špatně :-) Kolegové? Děkuji.
Offline
#11 10. 05. 2013 11:55
Re: obsah plochy
↑ jelena:
pravda je to nejednoznacne zadane, dokonca by odpoved mohla byt aj nekonecno, ale to predpokladame, ze sa asi nemysli. A ked uz tak hadame, tak ja by som sa priklonil k tvojej moznosti 1, lebo inak by bola podmienka  zbytocna.
zbytocna.
↑ dugbutabi:
co? vyzera byt zadane ako dalsia podmienka ...
vyzera byt zadane ako dalsia podmienka ...
Offline
#13 10. 05. 2013 12:11
Re: obsah plochy
↑ dugbutabi:
no moze byt aj taka interpretacia ... preto nemam rad taketo nejednoznacne zadania. neviem o kolko viac roboty da napisat to korektne. Napr. takto
vypocitajte obsah plochy danej nerovnostami:  a
a 
Offline
#15 11. 05. 2013 00:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: obsah plochy
↑ jendula11:
dle debaty kolegů ↑ dugbutabi: a ↑ Brano: se jeví, že podmínka  pouze určuje, že obrazec bude v 1. a 2. kvadrantech (jelikož nemáme přímku
pouze určuje, že obrazec bude v 1. a 2. kvadrantech (jelikož nemáme přímku  , nemůžeme omezit plochu "otevřená kniha"). Potom to vypadá na variantu a souhlasí to s návrhem, co jsi napsal v příspěvku ↑ 3:, jen drobnost - jelikož je obrázek symetrický, stačí počítat jen pravou polovinu od
, nemůžeme omezit plochu "otevřená kniha"). Potom to vypadá na variantu a souhlasí to s návrhem, co jsi napsal v příspěvku ↑ 3:, jen drobnost - jelikož je obrázek symetrický, stačí počítat jen pravou polovinu od  do
do 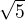 a výsledek vynásobit 2.
a výsledek vynásobit 2.
↑ Brano:
ještě přesnější je  a
a  , děkuji za posun tématu :-)
, děkuji za posun tématu :-)
Offline
#16 11. 05. 2013 00:43
Re: obsah plochy
↑ jelena:
hmm.. preco by neostre nerovnosti mali byt preferovane?
ja mam radsej ostre
1) obsah to nemeni
2) vyrok plocha ohranicena blabla ... neznamena, ze tam je aj ta hranica (ani ze tam nie je)
3) ostra nerovnost ma menej ciarok a v TeXu je to jeden symbol oproti trom
Offline
#17 11. 05. 2013 10:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: obsah plochy
↑ Brano:
a proč ne?
ja mam radsej ostre
já mám nejraději, když prší (jako teď), nebo sněží :-) Jelikož matematik nejsem ani vzdáleně, tak pokud si nevím rady, tak v českém prostředí se podívám do Rektoryse, v ruském - do Фихтенгольца а oba mi říkají, že pro výpočet obsahu nerovností ho zadávající musí být neostré. Konec konců v tomto zadání pravě ostrá nerovnost  může být argumentem, proč se zvolila zrovna taková oblast k výpočtu. Tak :-)
může být argumentem, proč se zvolila zrovna taková oblast k výpočtu. Tak :-)
Se mnou bohužel (naštěstí) o matematice nepodiskutuješ, ve mém případě by to padalo na zcela neúrodnou půdu, spíš s kolegy.
ostra nerovnost ma menej ciarok a v TeXu je to jeden symbol oproti trom
tak to bych jako argument brala. Zdravím.
Offline
#18 11. 05. 2013 18:37 — Editoval Brano (11. 05. 2013 18:39)
Re: obsah plochy
Dobre aby to nevyznelo nejak nejasne.
Nie nemusia to byt neostre nerovnosti, dokonca jedna moze byt neostra a ina ostra. Obsah je miera mnoziny u ktorej teda staci ked je meratelna. Hranica otvorenej mnoziny (co je tento) pripad je mnozina s nulovou mierou takze kvoli uplnosti Lebesgueovej miery si mozme pridat (resp. ubrat) jej lubovolny kusok a mnozina ostane stale meratelna a jej miera sa nezmeni.
PS: predpokladam, ze ak v uvedenej literature vyzaduju neostru nerovnost, tak je to ich preferencia kvoli jednoduchosti vykladu ale nieco take.
Offline
#19 11. 05. 2013 23:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: obsah plochy
Děkuji, mně je to cca jasné.
↑ Brano:
PS: predpokladam, ze ak v uvedenej literature vyzaduju neostru nerovnost, tak je to ich preferencia kvoli jednoduchosti vykladu ale nieco take.
ne, že by vyžadovali, ale přesně, jak píšeš, dokonce v tom smyslu je i poznámka v ruském textu, že pro názornost výkladu.
Co mne vážně zajímá, zda účet na Mat. fóru patří u kolegy ↑ jendula11: k rodinnému stříbru a která generace již účet využívá? :-)
Offline

