Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 04. 2013 16:53 — Editoval Anonymystik (30. 04. 2013 16:53)
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Dokážete sečíst řadu
Zdravím.
Včera jsem si trochu hrál a vymyslel jsem následující úložku: pro přirozené číslo  mějme konečnou řadu
mějme konečnou řadu  . Podaří se vám ji sečíst?
. Podaří se vám ji sečíst?
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#3 02. 05. 2013 10:52
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Dokážete sečíst řadu
Výborně - hypotéza je správná. Ještě je potřeba ji dokázat.
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#4 08. 05. 2013 15:07 — Editoval Anonymystik (08. 05. 2013 15:08)
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Dokážete sečíst řadu
Tak to vypadá, že úlohu se nikomu nechce řešit. Dám sem pro zájemnce hint:
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#5 09. 05. 2013 20:41
Re: Dokážete sečíst řadu
Toto je moj tisici prispevok, tak som chcel vyriesit nejaku peknu ulohu. Moje riesenie sice nie je stredoskolske, ale mne sa vcelku paci.
Trosku sa tu budeme hrat s vytvarajucimi funkciami. Vytvarajuca funkcia pre kombinacne cisla je znama.
kde
Vytvorme podobne funkcie pre variacie

Ciastocny sucet radu exponencialnej funkcie sa niekedy znaci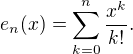
Potom  . Lahhko sa vidi, ze
. Lahhko sa vidi, ze a teda
a teda
Vyjadrime si  pomocou
pomocou  - v definicii
- v definicii  substituujme
substituujme 

a pouzijuc 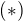 vypocitajme
vypocitajme a teda
a teda
predelme obe strany  a dostaneme
a dostaneme
PS: Ak by niekto chcel nejaky kompaktnejsi zapis tych vytvarajucich funkcii tak moze uvazit .
.
Lahko sa overi, ze 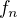 aj
aj  su riesenia rovnice
su riesenia rovnice a teda
a teda  .
.
Offline
#6 10. 05. 2013 00:08 — Editoval Anonymystik (10. 05. 2013 00:14)
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Dokážete sečíst řadu
↑ Brano: Ahoj. Několik poznámek k tvému důkazu:
- důkaz je správně
- protože nejsem s generujícími funkcemi moc kamarád, dalo mi místy práci důkaz sledovat. Každý jednotlivý krok je ale správně
- důkaz je zajímavý
- důkaz mi připadá dost trikový a nevím, jestli bych na něj přišel (aniž bych byl zrovna osvícen). Každopádně je chytré využít vlastností binomické věty a derivování exponenciály.
- za svůj důkaz dostáváš ode mě body do reputace a upřímný obdiv.
- jinak gratuluji k 1000. příspěvku!
Dokončení mého vlastního důkazu:
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#7 10. 05. 2013 01:01 — Editoval Brano (10. 05. 2013 01:11)
Re: Dokážete sečíst řadu
↑ Anonymystik:
Co sa tyka trikovosti - V podstate to je taky "brute force" pristup. Tak nejak hned (mozno kvoli tvojmu hintu) sa mi zdalo prirodzene zaujimat sa o funkciu  - tu som dal spocitat W|A ten mi vyhodil vysledok cez hornu neuplnu Gamma funkciu ako som uviedol v PS - tak som si to dokazal a postupne zjednodusoval az som prisieil na to ze to "explicitne" vyjadrenie ani netreba
- tu som dal spocitat W|A ten mi vyhodil vysledok cez hornu neuplnu Gamma funkciu ako som uviedol v PS - tak som si to dokazal a postupne zjednodusoval az som prisieil na to ze to "explicitne" vyjadrenie ani netreba
ale samozrejme zjednodusit to do formy ktoru som spisal chvilku trvalo ... ja casto davam prednost "technickej jednoduchosti" vykladu pred jeho "intuitivnostou" hlavne asi preto, ze sa mi nechce vela pisat
inak tiez sa mi dost paci tvoj postup, ja som zase s kombinatorikou nikdy nebol kamarat :-)
Offline
#8 11. 05. 2013 20:44
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Dokážete sečíst řadu
↑ Anonymystik:
Ahoj, pěkné. Vzorec trošku připomíná hodnotu počtu koster (stromů) na n vrcholech. Možná by bylo zajímavé se pokusit o důkaz tohoto tvrzení na základě Tvé identity.
"Máte úhel beta." "No to nemám."
Offline

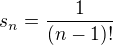
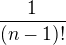 . Mělo by tedy platit
. Mělo by tedy platit 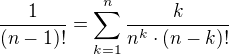 . Chceme, aby nalevo i napravo byla pouze celá čísla. Nejprve se napravo zbavíme ve jmenovateli toho
. Chceme, aby nalevo i napravo byla pouze celá čísla. Nejprve se napravo zbavíme ve jmenovateli toho  . Jak to uděláme? No pokud
. Jak to uděláme? No pokud  běží od
běží od  do
do 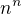 , čímž napravo získáme
, čímž napravo získáme  , kde
, kde 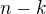 je pro
je pro  vždy nezáporné, tedy
vždy nezáporné, tedy 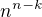 je celé číslo. Teď tedy máme vztah
je celé číslo. Teď tedy máme vztah  .
. 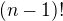 . Co s tím? Přenásobme tedy obě strany rovnice tímto výrazem, přičemž napravo tento výraz schovejme dovnitř sumy. Získáme toto:
. Co s tím? Přenásobme tedy obě strany rovnice tímto výrazem, přičemž napravo tento výraz schovejme dovnitř sumy. Získáme toto:  .
. 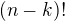 . V čitateli vidíme výraz
. V čitateli vidíme výraz  , tak
, tak  by šlo interpretovat jako počet
by šlo interpretovat jako počet 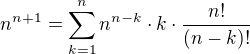 . Nalevo i napravo vystupují nyní pouze celá čísla, a tutíž půjde kombinatorická interpretace použít. A to už nechám na vás!
. Nalevo i napravo vystupují nyní pouze celá čísla, a tutíž půjde kombinatorická interpretace použít. A to už nechám na vás!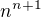 se dá interpretovat jako počet možných hesel, které jsou tvořeny
se dá interpretovat jako počet možných hesel, které jsou tvořeny  znaky, přičemž každý znak je vybrán z
znaky, přičemž každý znak je vybrán z  -tý znak se vybere z těch znaků, které už byly použity. Kolik takových hesel s touto podmínkou existuje? Zjevně prvních
-tý znak se vybere z těch znaků, které už byly použity. Kolik takových hesel s touto podmínkou existuje? Zjevně prvních 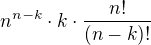 . Takže existuje právě
. Takže existuje právě  -té pozici. Žádná jiná možnost není. Proto vysčítáním výrazů
-té pozici. Žádná jiná možnost není. Proto vysčítáním výrazů