Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » L_p normy a "nenormy" v R^n (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 05. 2013 12:58
L_p normy a "nenormy" v R^n
Nazdar kolegové, po dlouhý době bych potřeboval radu. Pro 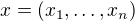 a
a  definujme
definujme 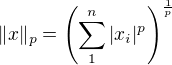 . Pro
. Pro  jde o normy, pro
jde o normy, pro  to není subaditivní, má to ale nějakej název? Dále pro
to není subaditivní, má to ale nějakej název? Dále pro  jsou všechny ty normy ekvivalentní, to je známej fakt, a jsem si celkem jistej, že i pro
jsou všechny ty normy ekvivalentní, to je známej fakt, a jsem si celkem jistej, že i pro  jsou ty "nenormy" s nima taky "ekvivalentní" - k tomu bych ale potřeboval nějakej zdroj, kterej bych mohl ocitovat v dipomce. Nevíte o něčem?
jsou ty "nenormy" s nima taky "ekvivalentní" - k tomu bych ale potřeboval nějakej zdroj, kterej bych mohl ocitovat v dipomce. Nevíte o něčem?
Offline
- (téma jako vyřešené označil(a) Stýv)
#4 10. 05. 2013 17:18 — Editoval vanok (10. 05. 2013 17:21)
Re: L_p normy a "nenormy" v R^n
Ahoj ↑ Stýv:,
Ide o kvazi- normu
http://en.wikipedia.org/wiki/Quasinorm
Pozri aj toto
http://books.google.fr/books?id=7RC9FPk … mp;f=false
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 10. 05. 2013 20:14 — Editoval Brano (10. 05. 2013 20:16)
Re: L_p normy a "nenormy" v R^n
↑ Stýv:
no ja som presvedceny ze to je trivialne ... ved podme to skusit zdovodnit a uvidime ci tam nemam niekde chybu
0) ujasnenie: topologia je generovana gulami 
1) na ekvivalentnost s euklidovskou normou staci dokazat, ze pre jednotkovu gulu  sa daju najst euklidovske gule
sa daju najst euklidovske gule 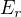 ,
, 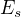 kde
kde  ; take, ze
; take, ze 
2) na to staci ukazat, ze 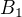 je v euklidovskej norme ohranicena (ocividne) a otvorena - to vyplyva zo spojitosti (Euklidovskej)
je v euklidovskej norme ohranicena (ocividne) a otvorena - to vyplyva zo spojitosti (Euklidovskej) 
Offline
#6 10. 05. 2013 20:35
Re: L_p normy a "nenormy" v R^n
Offline
#7 10. 05. 2013 21:10
Re: L_p normy a "nenormy" v R^n
↑ Stýv:,
Toto je tiez vdaka Google.
http://www.ams.org/journals/tran/1966-1 … 3437-3.pdf
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » L_p normy a "nenormy" v R^n (TOTO TÉMA JE VYŘEŠENÉ)
