Matematické Fórum

Adulka · 12. 05. 2013 19:22

Vyřešte průběh funkce bez infexních bodů, bez konvexních am konkávních.

f: $y=\frac{x^{4}-2x^{2}}{4}$

takže $D(f)=R$
$\frac{-4x^{4}+2x^{2}}{4}=\frac{4x^{4}-2x^{2}}{4}$
$-(\frac{4x^{4}-2x^{2}}{4})=\frac{4x^{4}-2x^{2}}{4}$
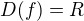
takže funkce je lichá??

zjistím si $P_{x}$ a $P_{y}$
$0=\frac{4x^{4}-2x^{2}}{4}$
$0=\frac{2x^{2}(2x^{2}-1)}{4}$
zbavím se zlomku
$0={2x^{2}(2x^{2}-1)}$
a jak to mam dodělat zase roznásobit?? neb jak zjistim to x?
a $P_{y}[0;0]$

dederivuji:
$y=\frac{(x^{4}-2x^{2})*0-(4x^{3}-4x)*4}{16}$
y $\frac{-16x^{3}+16x}{16}$
a jhak dál.??
a jak bude vypadat graf??

vanok · 12. 05. 2013 19:48 — Editoval vanok (12. 05. 2013 19:48)

ta funkcie je parna (suda)
lebo
$f(x)=\frac{(-x)^{4}-2(-x)^{2}}{4}=\frac{x^{4}-2x^{2}}{4}=f(x)$ pre kazde realne $x$

Co sa tyka jej variacii, najdi prvu derivaciu, prestuduj ako je to zo znamienkamy tej derivacii a z toho na koniec, najdi intervaly, kde tvoja funkcia je klesajuca alebo stupajuca.

Adulka · 12. 05. 2013 20:04

↑ vanok:
no to jsem zderivovala a vyslo mi $y^{,}=\frac{-16x^{3}+16x}{16}$

bonifax · 12. 05. 2013 20:52

↑ Adulka:

Ahoj,

$P_x:$ => za y dosadíš 0

Té 4ce na začátku nerozumím.

$P_y:$ => za x dosadíš 0 a vyjdou ti kořeny.

Ta derivace není dobře, jelikož si špatně použila vzorec pro derivaci podílu. Navíc v tomto případě to půjde mnohem snadněji, pač ve jmenovateli je konstanta. Stačilo zderivovat čitatel a pak roztrhnout na dva zlomky nebo rozdělit na dva zlomky rovnou a pak zderivovat.

Dále: vypočítat limity v nekonečnu a v 0, lokální extrémy, monotonost, asymptoty atd..

vanok · 12. 05. 2013 20:58

↑ Adulka:,
Ta derivacie je chybna.
Malo to dat : $f'( x)=\frac{(x^{4})'-2(x^{2})'}{4}= \frac{4x^3-2\cdot 2x}4=...$ pokracuj

Adulka · 12. 05. 2013 22:54

↑ vanok:
dit se toto derivuje podle vzorce ne snad?? horni*derivacedolni minus derivace horni*dolní lomeno dplmí na druhou...

vanok · 12. 05. 2013 23:12

Ano, ale tu mas v menovateli konstantu.
( a iste ste videli, ze derivacia konstanty je nula,
a potom, ze (af(x))'=a f'(x) , kde a je konstanta co znamena ze funkcia nasobena konstantou a, ma derivaciu, toraa je derivacia funkcie nasobenej konstantou a )

Matematické Fórum

#1 12. 05. 2013 19:22

derivace průběh funkce

#2 12. 05. 2013 19:48 — Editoval vanok (12. 05. 2013 19:48)

Re: derivace průběh funkce

#3 12. 05. 2013 20:04

Re: derivace průběh funkce

#4 12. 05. 2013 20:52

Re: derivace průběh funkce

#5 12. 05. 2013 20:58

Re: derivace průběh funkce

#6 12. 05. 2013 22:54

Re: derivace průběh funkce

#7 12. 05. 2013 23:12

Re: derivace průběh funkce

Zápatí