Matematické Fórum

kolejo · 12. 05. 2013 12:57

Dobrý den,
mám tu jeden takový důkaz a rád bych se tu s tím rozšířil:

$\text{Pomocí věty o střední hodnotě dokažte následující verzi l'Hopitalova pravidla:}$
$\text {Je-li }\lim_{x\to a_+}f(x)=\lim_{x\to a_+}g(x)=\infty$
$\text{a tato limita existuje: } \lim_{x\to a_+}\frac{f'(x)}{g'(x)}$
$\text{pak } \lim_{x\to a_+}\frac{f(x)}{g(x)} =\lim_{x\to a_+}\frac{f'(x)}{g'(x)}$

Hledal jsem různě na internetu, Dr.Math nebo jak se jmenuje, našel jsem aji toto:
http://www.mathdb.org/resource_sharing/ … l_rule.pdf

Mám to dokázat pomocí tohoto:
existuje c v intervalu (a,b) takové, že pro f,g spojité na [a,b] (jejichž derivace na tom intervalu existují a g'(x) je nenulová pro každé x)
$\frac{f'(c)}{g'(c)}=\frac{f(b)-f(a)}{g(b)-g(a)}$

Mohl bych tvrdit, že mám f(a)=0 a g(a)=0? To by pak bylo jednoduché a to by pak nešlo o tuto verzi onoho pravidla. Tedy tudy ne.

Označím $\lim_{x\to a_+}\frac{f'(x)}{g'(x)}=L$
Potom ukážu $\lim_{x\to a_+}\frac{f(x)}{g(x)}=L$

Využiji nějak toho, že se ty limity f,g sobě rovnají?
Nevím, dál nevím, tady už to tedy nechám...a poprosím o pomoc.
Moc děkuji,
kolejo

Brano · 12. 05. 2013 13:26 — Editoval Brano (12. 05. 2013 14:49)

ten dokaz nie je uplne trivialny. mozes si ho pozriet na wiki.

edit: na tomto fore su nejak divne kodovane apostrofy a asi preto nefunguje ten odkaz (teda aspon mne) a neviem to opravit, ale da sa to vygooglit: "lhopital wiki" a v anglickej verzii clanku sekcia: general proof

kolejo · 12. 05. 2013 13:30

↑ Brano:
Ano, děkuji.
K tomu důkazu tam jsem hledáním dospěl, tak se na něj pozorněji ještě podívám. Mám totiž problém s tím, že obě ty limity se rovnají nekonečnu a nejen g. Tímto by to mělo být o dost jednodušší, tak se ptám, v čem to je.

Brano · 12. 05. 2013 14:04

teraz nejak neviem co si tym chcel povedat.
L'H plati v pripadoch ak $f,g\to 0$ a $f,g\to\pm\infty$
pripad $f,g\to c\not=0$ nie je zaujimavy, lebo potom trivialne $f/g\to 1$ a dokonca tvrdenie z L'H samozrejme nemusi platit; napr.
$\lim_{x\to 0}\frac{1+x}{1+2x}\not=\frac{1}{2}$

kolejo · 12. 05. 2013 14:17

↑ Brano:
chcel som povedat, že $f,g\to \infty$ , že lim f=lim g=oo
v těch důkazech které nacházím se neřeší lim f. ale asi něco míjím, tedy...

no znovu a znovu se dívám na tu wikipedii a pomalu mi to dochází.
tak se dnes ještě ozvu s jakýmsi překladem důkazu pro fórum a pro mě, čímž pak téma budu moct uzavřít.
Děkuji za pomoc

Brano · 12. 05. 2013 15:01 — Editoval Brano (12. 05. 2013 15:02)

aha mal si na mysli toto?

netreba predpokladat, ze aj $|f|\to\infty$ aj $|g|\to\infty$ ale staci prepokladat iba, ze $|g|\to\infty$

to som si predtym neuvedomil, ale je to tak - trochu sa to da nahliadnut tak, ze ak by $|f|\to c<\infty$ potom by obe limity vysli jednoducho nula a teda efektivny dokaz limitu $f$ ani nebude spominat.

kolejo · 12. 05. 2013 15:03

Nó, alé... máme v zadání, že f->oo a g->oo. a lim f'/g' existuje
snad se chápeme správně.

Brano · 12. 05. 2013 15:08 — Editoval Brano (12. 05. 2013 15:10)

Ano jasne. ono sa to obvykle zvykne predpokladat,len to vyzera tak, ze to predpokladat netreba a da sa to dokazat aj bez toho. To nic nemeni na spravnosti tvrdenia.

Ak A implikuje C tak potom aj A&B implikuje C.

ps: a samozrejme predpoklad existencie $\lim\frac{f'}{g'}$ je podstatny, lem som ho predtym nevypisoval, lebo to som povazoval za samozrejme

kolejo · 12. 05. 2013 15:09

Aha, dobře, děkuji.

kolejo · 12. 05. 2013 15:55

↑ Brano:

tak jsem to právě z toho dodělal a nemá smysl sem z toho cokoliv psát, protože na nic nového jsem nepřišel, žádnou poznámku k tomu ještě nemám.

Třeba ale s něčím přijde Hanis, který se tu nejspíš večer zjeví, tedy téma ještě ponechám nevyřešené. (kdyby cokoliv kdokoliv někdo chtěl, tak je taky vítán)

Hanis · 12. 05. 2013 18:19

No já bych se to pokusil vyklepat tak, že když lim f'(x)->oo, tak limita 1/f'(x) jde do nuly atd. čímž bychom se dostali k tomu jednoduššímu důkazu.

Ale nevím, jestli je to korektní...

kolejo · 12. 05. 2013 18:23

Já to za korektní považuji.

Hanis · 12. 05. 2013 18:41

ok, snad to bude považovat za korektní i zbytek světa

vanok · 12. 05. 2013 19:20 — Editoval vanok (12. 05. 2013 19:38)

Pozri na tento dokaz

V neprazdnom intervale $]x, y[$ cast $]a, b$ existuje realne $c$ take, ze $\frac{f(x) - f(y)}{g(x) - g(y)}= \frac{f'(c)}{g'(c)}$ cize

$f(x) = (g(x) - g(y))\frac{f'(c)}{g'(c)} + f(y).$

Ak $g(x)\neq 0$

$\frac{f(x)}{g(x)} = \left(1 - \frac{g(y)}{g(x)}\right )\frac{f'(c)}{g'(c)} +\frac{f(y)}{g(x)}.$

Akoze $\lim_{t \to a^+} \frac{f'(t)}{g'(t)} = l$ ,a tiez akoze $c\in ]a, y[$ , mozme vybrat $y \in ]a, b[$ take ze $\frac{f'(c)}{g'(c)}$ je take blizke ako chceme k $l$

potom pre take $y$ ,akoze $g(x)$ ide k nekonecnu, mozme vzdy najst interval $]a, r[$ cast $]a, y[$ taky, ze $g(x)$ nie je nula a $\frac{g(y)}{g(x)}$ a $\frac{f(y)}{g(x)}$ take bizke k $0$ ako len chceme pre kazde $x \in$ ]a, r[.$

podla wikipedie

kolejo · 12. 05. 2013 19:33 — Editoval kolejo (12. 05. 2013 19:34)

↑ vanok:

Sice jsem to chvíli musel luštit, ale mezinárodnost matematiky zafungovala a mám to.
Děkuji moc

EDIT:
je to nakonec tedy velmi srozumitelné,
ještě jednou moc děkuji,
s pozdravem

vanok · 12. 05. 2013 19:40

↑ kolejo:
to je standardne pouzivany dokaz, zobral som to z wikipedie, a akoze som mily clovek, som ti to prelozil do slovenciny.
I ked je nutne sa ucit svetove jazyky.

Dobre pokracovanie.

kolejo · 12. 05. 2013 19:55

↑ vanok:

Ano, to jste. Díky, super.
Vztah, který chceme dokázat, z daného plyne docela zřejmě.

Brano · 13. 05. 2013 00:09

↑ Hanis:
no a ako to dokoncis, lebo napr. v uvahe typu
$\frac{f}{g}=\frac{1/g}{1/f}\sim\frac{-g'/g^2}{-f'/f^2}=\frac{g'}{f'}\frac{f^2}{g^2}$

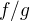cize ak mas zarucenu existenciu limit $f'/g'$ a $f/g$ tak sa rovnaju, ale L'H hovori viac t.j. ak $f'/g'$ existuje potom $f/g$ existuje a rovnaju sa.

Hanis · 13. 05. 2013 07:10

Jasně, to je mnohem slabší tvrzení. Děkuji za opravu, neuvědomil jsme si to...

Matematické Fórum

#1 12. 05. 2013 12:57

Důkaz, verze l'Hopitalova pravidla

#2 12. 05. 2013 13:26 — Editoval Brano (12. 05. 2013 14:49)

Re: Důkaz, verze l'Hopitalova pravidla

#3 12. 05. 2013 13:30

Re: Důkaz, verze l'Hopitalova pravidla

#4 12. 05. 2013 14:04

Re: Důkaz, verze l'Hopitalova pravidla

#5 12. 05. 2013 14:17

Re: Důkaz, verze l'Hopitalova pravidla

#6 12. 05. 2013 15:01 — Editoval Brano (12. 05. 2013 15:02)

Re: Důkaz, verze l'Hopitalova pravidla

#7 12. 05. 2013 15:03

Re: Důkaz, verze l'Hopitalova pravidla

#8 12. 05. 2013 15:08 — Editoval Brano (12. 05. 2013 15:10)

Re: Důkaz, verze l'Hopitalova pravidla

#9 12. 05. 2013 15:09

Re: Důkaz, verze l'Hopitalova pravidla

#10 12. 05. 2013 15:55

Re: Důkaz, verze l'Hopitalova pravidla

#11 12. 05. 2013 18:19

Re: Důkaz, verze l'Hopitalova pravidla

#12 12. 05. 2013 18:23

Re: Důkaz, verze l'Hopitalova pravidla

#13 12. 05. 2013 18:41

Re: Důkaz, verze l'Hopitalova pravidla

#14 12. 05. 2013 19:20 — Editoval vanok (12. 05. 2013 19:38)

Re: Důkaz, verze l'Hopitalova pravidla

#15 12. 05. 2013 19:33 — Editoval kolejo (12. 05. 2013 19:34)

Re: Důkaz, verze l'Hopitalova pravidla

#16 12. 05. 2013 19:40

Re: Důkaz, verze l'Hopitalova pravidla

#17 12. 05. 2013 19:55

Re: Důkaz, verze l'Hopitalova pravidla

#18 13. 05. 2013 00:09

Re: Důkaz, verze l'Hopitalova pravidla

#19 13. 05. 2013 07:10

Re: Důkaz, verze l'Hopitalova pravidla

Zápatí