Matematické Fórum

rikimara · 25. 05. 2012 07:50

Zdravím,
potřeboval bych pomoc s jedním příkladem na rezoluční metodu. Zadání je takové:

Platí $M \models \varphi$ ?
$M = \{P\wedge Q\Rightarrow R, P\wedge (R\vee S),\neg(Q\Rightarrow (P\wedge S)),\neg(Q\Leftrightarrow (P\wedge S))\}$
$\varphi = (P\wedge Q)\vee (R\wedge S)$

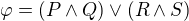
Princip chápu. Zneguji fí a převedu do CNF tvaru. Do CNF převedu i množinu M. A poté použiju rezoluční algoritmus. Pokud to bude splnitelné, tak neplatí. Pokud to splnitelné nebude, tak platí. Můj problém je s převedením výrazu z množony M do CNF, konkrétně 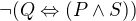$\neg(Q\Leftrightarrow (P\wedge S))$

Pomocí úprav se mi to do CNF nepodařilo převést, ač vím, že to jít musí. :)
Děkuji mockrát za pomoc.

Tychi · 25. 05. 2012 08:44

Já jsem se pomocí transformace ekvivalence a de Morgana dostala k
$(\neg Q\vee\neg P\vee \neg S)\wedge Q \wedge P\wedge S$
To se mi jeví jako CNF. Otázkou je, jestli jsem si to zase někde nezjednodušila

zrzex · 15. 05. 2013 15:28

Ahoj, při učení na zkoužku jsem narazil na stejný problém jako tady kolega předemnou. Podařilo se mi dospět k tomuto...
$(Q \wedge \neg P) \vee (Q \wedge \neg S) \vee (P \wedge S \wedge \neg Q)$

i když to asi jako CNF moc nevypadá, ale dál se za boha nemůžu dostat, určitě dělám něco špatně. Nebyl by někdo tak laskav a nerozepsal by, jak se krok po kroku lze dostat ke správnému výsledku ?

Děkuji za pomoc.

Matematické Fórum

#1 25. 05. 2012 07:50

Převod formule do CNF

#2 25. 05. 2012 08:44

Re: Převod formule do CNF

#3 15. 05. 2013 15:28

Re: Převod formule do CNF

Zápatí