Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 20. 05. 2013 20:33
Re: nerovnice s absolutní hodnoutou
↑ pantucnak:
a nebo muzes celou nerovnici vynasobit vyrazem 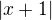 , protoze je vzdy kladny a nezmeni znameko nerovnice. nemusis se trapit se zlomkama ;)
, protoze je vzdy kladny a nezmeni znameko nerovnice. nemusis se trapit se zlomkama ;)
Offline

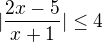
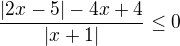 a nevím co mám dělat s tou absolutní hodnotou v čitateli. může mi někdo poradit?
a nevím co mám dělat s tou absolutní hodnotou v čitateli. může mi někdo poradit?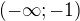 ,
, ![kopírovat do textarea $(-1;5/2]$](/mathtex/f8/f8ea24440ca234e4231e041d739eedca.gif) a
a 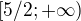 a pak to řešíš jako obyč nerovnici- např. na
a pak to řešíš jako obyč nerovnici- např. na 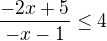 .
.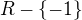 , do tabuľky zapísať intervaly,...
, do tabuľky zapísať intervaly,...