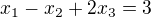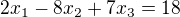Matematické Fórum

Nejlépe to půjde přes matice - přepiš si to na matici přidružené homogenní rovnice a rozšířenou matici. Pokud budou mít obě matice pro nějaké hodnoty a hodnost 3, má soustava právě jedno řešení. Pokud budou mít obě matice hodnost menší než dva ale stejnou, má pro danou hodnotu parametru a soustava nekonečně mnoho řešení. No a pokud se budou hodnosti lišit, nemá pro dané a soustava řešení.

Pokud mi to po ránu myslí, mohl bys použít i fintu spočívající v tom, že a je jen v jedné rovnici. Vyřeš si první dvě rovnice - vyjde ti řešení závislé na jednom parametru t. To řešení si dosaď do poslední rovnice a sleduj, jak ti pro různé hodnoty a bude vycházet 0=0 (nekonečně mnoho řešení dané řešením prvních dvou rovnic), 1=0 (nemá řešení) a t=umtydumty(a) (právě jedno řešení).