Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 05. 2013 13:17
arimetnicke postupnosti
Dnes tu davam toto pekne cvicenie:
Nech 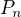 je mnozina pozitivnych nenulovych celych cisiel, ktore su mensie ako
je mnozina pozitivnych nenulovych celych cisiel, ktore su mensie ako  a aj nesudelitelne z
a aj nesudelitelne z  .
.
Pre ktore  , prvky z
, prvky z 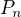 tvoria (konecnu) arimetnicku postupnost?
tvoria (konecnu) arimetnicku postupnost?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 20. 05. 2013 22:53 — Editoval liamlim (20. 05. 2013 22:57) Příspěvek uživatele liamlim byl skryt uživatelem liamlim. Důvod: Není správně
#3 23. 05. 2013 18:49 — Editoval vanok (23. 05. 2013 18:52)
Re: arimetnicke postupnosti
Zaciatok riesenia: ( budem uvazovat, len aritmeticke postupnosti, ktore maju aspon 3 cleny)
1) ak n je neparne prvocislo, tak 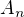 , tvori aritmeticka postupnost
, tvori aritmeticka postupnost 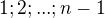
Poznamka, aby 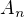 mala ( v tomto pripade) aspon tri prvky, treba
mala ( v tomto pripade) aspon tri prvky, treba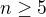 .
.
2)je jednoduche overit, ze pre ine neparne cisla 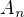 netvori aritmeticku postupnost.
netvori aritmeticku postupnost.
3) tu dokazeme, ze iba  kde
kde 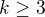 vyhovuju
vyhovuju
Dufam, ze tuto cast tu niekto dokaze.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 23. 05. 2013 23:02 — Editoval OiBobik (23. 05. 2013 23:14)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: arimetnicke postupnosti
↑ vanok:
Ahoj,
mám to tu rozepsané ze včerejška, ale kvůli zkouškovému příliš nestíhám. Tak to sem hodím a doufám, že během zítřka to dopíšu:
(uvažuju teda i případ dvoučlenných posloupností)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 25. 05. 2013 14:05 — Editoval vanok (25. 05. 2013 14:07)
Re: arimetnicke postupnosti
Tu dam jedno riesenie poslednej otazky, pozriet len po vyrieseni cvicenia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 25. 05. 2013 18:53 — Editoval OiBobik (25. 05. 2013 19:14)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: arimetnicke postupnosti
Tady je to dokončení mého postupu:
Je to trochu kostrbaté, ale na druhou stranu, dost přirozené.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
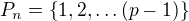 ) a
) a  (pak
(pak  ). Také dost triviálně to platí pro
). Také dost triviálně to platí pro 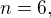 kdy
kdy 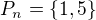 .
.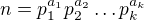 , kde
, kde  .
. jsou jistě nesoudělná s
jsou jistě nesoudělná s  není. Pokud tedy
není. Pokud tedy 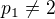 , nemůžou čísla nesoudělná s
, nemůžou čísla nesoudělná s 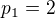 .
. , obsahuje
, obsahuje  . Pak už nutně musí obsahovat všechna lichá čísla menší než
. Pak už nutně musí obsahovat všechna lichá čísla menší než  je liché číslo menší než
je liché číslo menší než 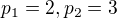 , ale
, ale  , tedy
, tedy 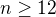 . Jelikož je pak
. Jelikož je pak  a je soudělná, nutně musí být číslo
a je soudělná, nutně musí být číslo 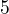 soudělné - tedy nutně
soudělné - tedy nutně 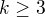 a
a  .
. a
a  .
.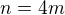 ,
,  su nesudelitelne s
su nesudelitelne s 
 (kde
(kde  ) a neparne cislo
) a neparne cislo 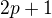 nie je nesudelitelne z
nie je nesudelitelne z 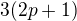 ).
).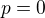 ,
, 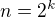 , mame okamzite, ze vyhovuje, ak
, mame okamzite, ze vyhovuje, ak 
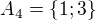 ma len dva prvky )
ma len dva prvky )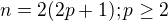
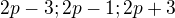 su nesudelitelne z
su nesudelitelne z  deli
deli 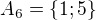 ma len dva prvky )
ma len dva prvky )
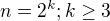
 .
. , už obsahuje i
, už obsahuje i  , spor. Tedy lze předpokládat
, spor. Tedy lze předpokládat 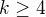 a
a 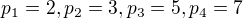 .
. je nejmenší číslo nesoudělné s
je nejmenší číslo nesoudělné s  prvočíslo.
prvočíslo. a prvočísla
a prvočísla  ze zápisu výše je prvních
ze zápisu výše je prvních  nejmenších prvočísel.
nejmenších prvočísel. , nesoudělné s
, nesoudělné s 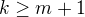 a
a  , čímž dostaneme (indukcí), že
, čímž dostaneme (indukcí), že  :
: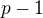 dělitelné součinem
dělitelné součinem 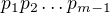 . To by ovšem znamenalo, že mezi
. To by ovšem znamenalo, že mezi  a
a  nejsou žádná prvočísla vyjma
nejsou žádná prvočísla vyjma 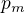 , speciálně pak, že
, speciálně pak, že 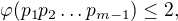 to je spor (kde
to je spor (kde  je Eulerova fce).
je Eulerova fce). . Pak
. Pak  . S trochou snahy se dá ukázat, že
. S trochou snahy se dá ukázat, že  . Tedy kdyby
. Tedy kdyby 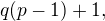 což je ovšem číslo dělitelné
což je ovšem číslo dělitelné  , tedy soudělné s
, tedy soudělné s