Matematické Fórum

Blackflower · 25. 05. 2013 11:21

Ahojte,
vedel by mi niekto pomôcť s týmto príkladom?

Charakteristickú funkciu pre vektor $X=(X_1,...,X_n)^T$ sme mali definovanú asi takto:
$\varphi _x(t)=E(e^{it^TX})=E(e^{i\sum_{j=1}^{n}t_jX_j})$
Ja som si to skúsila podľa toho rozpísať:
$Z=(X,Y)^T$
$\varphi _Z(t)=E(e^{it^TZ})=E(e^{i\sum_{j=1}^{2}t_jZ_j})=E(e^{i(t_1X+t_2Y)})$
Teraz fakt neviem, ako ďalej, nie som si ani istá, že vôbec toto je dobre.
Vopred vďaka za každú radu.

Brano · 25. 05. 2013 13:17 — Editoval Brano (26. 05. 2013 13:55)

mas
$\varphi_Z(t_1,t_2)=E$e^{i(t_1X+t_2Y)}$$
a teda
$\varphi_Z(t_1,0)=E$e^{it_1X}$=\varphi_X(t_1)$
na $cov$ skus uvazovat
$\frac{\partial^2\varphi_Z}{\partial t_1\partial t_2}(0,0)$
a aj prve derivacie a prides na to :-)

Blackflower

↑ Brano: Môže to vyzerať takto alebo som úplne mimo?
$iE(X)=\frac{\partial \varphi _Z}{\partial t_1}=iE(e^{it_1X+it_2Y}\cdot X)$
$iE(Y)=\frac{\partial \varphi _Z}{\partial t_2}=iE(e^{it_1X+it_2Y}\cdot Y)$
Položím t=0 a dopočítam strednú hodnotu, len to vychádza nejako divne.
Keď zderivujem prvý výraz podľa $t_2$ , dostanem $i^2E(XY)=i^2E(e^{it_1X+it_2Y}\cdot XY)$ .
Neviem teda, či to je dobrá úvaha, mám v tom slušný zmätok.

Brano · 26. 05. 2013 02:22

tato rovnost
$iE(X)=\frac{\partial \varphi _Z}{\partial t_1}=iE(e^{it_1X+it_2Y}\cdot X)$
neplati, aj ked to samozrejme myslis uplne dobre, ale treba to aj spravne zapisat
napr.
$\frac{\partial \varphi _Z}{\partial t_1}=iE(e^{it_1X+it_2Y}\cdot X)$
a teda
$iE(X)=\frac{\partial \varphi _Z}{\partial t_1}(0,0)$

Blackflower · 26. 05. 2013 12:40

↑ Brano: Ja už neviem...
$iE(X)=\frac{\partial \varphi _Z}{\partial t_1}(0,0)=\frac{\partial \varphi _Z}{\partial t_1}=iE(e^{i0X+i0Y}\cdot X)=iE(X)$
To asi nebude dobre...

Brano · 26. 05. 2013 13:48 — Editoval Brano (26. 05. 2013 13:54)

↑ Blackflower:
no tak este raz - myslienka je uplne spravne - mal som vyhrady voci zapisu ta cast co neplati teraz je toto
$\frac{\partial \varphi _Z}{\partial t_1}(0,0)=\frac{\partial \varphi _Z}{\partial t_1}$
pretoze vlavo je cislo a vpravo je funkcia

napr. rovnost $\sin 0=\sin x$ tiez nie je vo vseobecnosti spravna

ale spravne je toto
$\frac{\partial \varphi _Z}{\partial t_1}(0,0)=iE(e^{i0X+i0Y}\cdot X)=iE(X)$

vysledok by teda mal byt
$\text{cov}(X,Y)=\frac{\partial\varphi_Z}{\partial t_1}(0,0)\frac{\partial\varphi_Z}{\partial t_2}(0,0)-\frac{\partial^2\varphi_Z}{\partial t_1 \partial t_2}(0,0)$

Blackflower

↑ Brano: Len ja mám pocit, že tam vychádza $iE(X)=iE(1\cdot X)$ a to isté pri ypsilone... tak teraz neviem... to mi v príklade ide iba o to, aby som z $iE(X)$ nejakými úpravami dostala opäť $iE(X)$ , to isté pri $E(Y)$ ? Mám aspoň dobre tú druhú deriváciu podľa obidvoch premenných? $\frac{\partial^2\varphi _Z}{\partial t_1 \partial t_2}=i^2E(e^{it_1X+it_2Y}\cdot XY)$

Brano · 26. 05. 2013 17:28

teraz nejak nechapem co sa ti nepaci na rovnosti $X=1\cdot X$
a ano toto
$\frac{\partial^2\varphi _Z}{\partial t_1 \partial t_2}=i^2E(e^{it_1X+it_2Y}\cdot XY)$
je samozrejmne spravne

Blackflower · 26. 05. 2013 17:30

↑ Brano: Ja som myslela, že mám dostať výsledok typu $E(X)=c$ , nejaké číslo, prípadne výraz s písmenkami...

Brano · 26. 05. 2013 22:52

↑ Blackflower:
vyraz
$\text{cov}(X,Y)=\frac{\partial\varphi_Z}{\partial t_1}(0,0)\frac{\partial\varphi_Z}{\partial t_2}(0,0)-\frac{\partial^2\varphi_Z}{\partial t_1 \partial t_2}(0,0)$
je konstanta a je to vyraz s pismenkami

Blackflower · 26. 05. 2013 22:54

↑ Brano: Ja už neviem... asi to nechajme tak, vychádzajú mi tam voloviny... ďakujem ti veľmi pekne za tvoju ochotu a čas.

Brano · 26. 05. 2013 23:11 — Editoval Brano (26. 05. 2013 23:20)

tak skusme este kompletny postup .. trosku si zoptomalizujem znacenie

$\partial_t=\frac{\partial}{\partial_t}$

definicia .. $\varphi(s,t)=E$e^{i(sX+tY)}$$
teda
$\partial_s\varphi(s,t)=E$e^{i(sX+tY)}iX$$
cize
$\partial_s\varphi(0,0)=iE$X$$
a podobne
$\partial_t\varphi(0,0)=iE$Y$$
a tiez
$\partial_s\partial_t\varphi(s,t)=E$e^{i(sX+tY)}iXiY$$
a teda
$\partial_s\partial_t\varphi(0,0)=-E$XY$$
nakoniec dostaneme
$\text{cov}(X,Y)=E(XY)-E(X)E(Y)=\partial_s\varphi(0,0)\partial_t\varphi(0,0)-\partial_s\partial_t\varphi(0,0)$

PS: nieviem ci problem sposobuje $\varphi$ vo vysledku, ale ved tam predsa nemoze nebyt kedze $\varphi$ je jedina informacia o rozdeleni 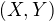$(X,Y)$ . Ak by tam nebola, tak to by znamenalo, ze $\cov(X,Y)$ by bolo vzdy rovnake cislo nezavisle na tom ake nahodne vektory si zvolis a to by bola somarina, nie?

Blackflower · 26. 05. 2013 23:21

↑ Brano: Už to asi chápem... čiže keby som mala danú nejakú konkrétnu charakteristickú funkciu, tak by mi ju stačilo zderivovať podľa všetkého možného a dosadiť do vzorca? Tým pádom cieľom príkladu bolo vlastne odvodiť ten vzorec?

Brano · 26. 05. 2013 23:27

no ved iste, zadanie hovorilo
pomocou nej (charakterisickej funkcie $(X,Y)$ ) vyjadrite ... $\text{cov}(X,Y)$

Blackflower · 26. 05. 2013 23:29

↑ Brano: Ja som hlúpa... hľadala som v tom kadečo a pritom to ani nebolo tak zložité... ešte raz ďakujem, si úplný pán!

Matematické Fórum

#1 25. 05. 2013 11:21

Charakteristická funkcia

#2 25. 05. 2013 13:17 — Editoval Brano (26. 05. 2013 13:55)

Re: Charakteristická funkcia

#3 25. 05. 2013 13:36 — Editoval Blackflower (25. 05. 2013 13:54)

Re: Charakteristická funkcia

#4 26. 05. 2013 02:22

Re: Charakteristická funkcia

#5 26. 05. 2013 12:40

Re: Charakteristická funkcia

#6 26. 05. 2013 13:48 — Editoval Brano (26. 05. 2013 13:54)

Re: Charakteristická funkcia

#7 26. 05. 2013 15:52 — Editoval Blackflower (26. 05. 2013 15:57)

Re: Charakteristická funkcia

#8 26. 05. 2013 17:28

Re: Charakteristická funkcia

#9 26. 05. 2013 17:30

Re: Charakteristická funkcia

#10 26. 05. 2013 22:52

Re: Charakteristická funkcia

#11 26. 05. 2013 22:54

Re: Charakteristická funkcia

#12 26. 05. 2013 23:11 — Editoval Brano (26. 05. 2013 23:20)

Re: Charakteristická funkcia

#13 26. 05. 2013 23:21

Re: Charakteristická funkcia

#14 26. 05. 2013 23:27

Re: Charakteristická funkcia

#15 26. 05. 2013 23:29

Re: Charakteristická funkcia

Zápatí