Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Analytičnost a derivace funkce definované integrálem
#1 01. 06. 2013 16:11
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Analytičnost a derivace funkce definované integrálem
Ahoj, mám problém z komplexní analýzy.
Mám funkci f definovanou pro  jako
jako
kde  je „hezká funkce“ (holomorfní na
je „hezká funkce“ (holomorfní na  až na konečnou množinu bodů, kde má funkce póly, můžeme určitě předpokládat, že póly nejsou na kladné reálné poloose a že na kladné reálné poloose nabývá funkce reálných hodnot) taková, že
až na konečnou množinu bodů, kde má funkce póly, můžeme určitě předpokládat, že póly nejsou na kladné reálné poloose a že na kladné reálné poloose nabývá funkce reálných hodnot) taková, že
Dá se nějak ukázat, že f se dá analyticky prodloužit do  ?
?
Funkce g by mohla být např.
kde  jsou nezáporná celá čísla,
jsou nezáporná celá čísla, 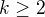 a
a  .
.
Dál by mě pak zajímalo, kdy bude n-tá derivace f v nule nulová. Snažím se totiž dokázat, že pro funkci g, která se v okolí nuly chová jako  se v Taylorově rozvoji f nebudou vyskytovat členy s lichou mocninou do řádu
se v Taylorově rozvoji f nebudou vyskytovat členy s lichou mocninou do řádu  včetně.
včetně.
(Předpoklady pro funkci g nejsou striktní, klidně uvažujte mírně pozměněné, ale určitě by jim měl vyhovovat uvedený příklad funkce g.)
Offline
#2 02. 06. 2013 19:08
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Analytičnost a derivace funkce definované integrálem

V druhém integrálu provedu substituci  .
.
Z toho je zřejmé, že v rozvoji  je
je
a
Ale co další členy rozvoje? Půjdou nějak jednoduše určit?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Analytičnost a derivace funkce definované integrálem