Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 06. 2013 21:40
goniometria
Dobry vecer, opat Vas zdravim ja s jednou prosbou :). Naskytol sa mi tu jeden priklad, v ktorom by som potreboval trochu usmernit.
Součin 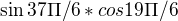 je roven číslu:
je roven číslu:
a) 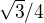
b) 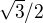
c) 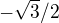
d)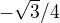
e) žádná z předchozích
Kedze sin aj cos maju periodu 2 pi, tak mi vznikol sucin 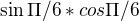 , co je
, co je 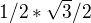 a vysledok mi vysiel
a vysledok mi vysiel 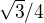 , lenze ma to byt D, tak by som rad vedel ako k tomu dospeli. A zaroven by som sa chcel spytat, keby v podobnom priklade bol podiel, tak ako by sa to riesilo (tu by myslim s podielom bol vysledok 1). Dakujem
, lenze ma to byt D, tak by som rad vedel ako k tomu dospeli. A zaroven by som sa chcel spytat, keby v podobnom priklade bol podiel, tak ako by sa to riesilo (tu by myslim s podielom bol vysledok 1). Dakujem
Offline
- (téma jako vyřešené označil(a) kvaso)
#4 02. 06. 2013 22:07 Příspěvek uživatele Jj byl skryt uživatelem Jj. Důvod: Pozdě - bezpředmětné
#5 02. 06. 2013 22:08
Re: goniometria
↑ kvaso: no právě že má periodu 2pi, takže znamená to, že kosinus každého čísla bude mít stejnou hodnotu, jako když k tomu číslu přičteme nějaký násobek 2pi. Takže postupuješ tak, že číslo 19pi/6 rozdělíš na součet maximálního násobku 2pi a nějkého čísla. V tomto případě : 19pi/6=2pi+7pi/6
V případě sinu to máš dobře.
Neberme rozum do hrsti, mohli bychom zjistit, že je prázdná.
Offline
#6 02. 06. 2013 23:02
Re: goniometria
Ou, az doteraz som to vzdy ratal automaticky aj sin aj cos bez odratavania 2pi a vzdy mi to vyslo (ako vidim robil som to zle), tak dakujem velmi pekne za ozrejmenie :).Len by som sa chcel este spytat, ze ako dospejem k tomu, ze 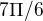 je
je 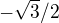 . Hodil som si to do jednotkovej kruznice, ktoru som rozdelil na sestiny. Kedze hovorime o cos tak 7pi/6 sa nachadza v zapornej casti. Je to spravne ? :)
. Hodil som si to do jednotkovej kruznice, ktoru som rozdelil na sestiny. Kedze hovorime o cos tak 7pi/6 sa nachadza v zapornej casti. Je to spravne ? :)
Offline
#7 03. 06. 2013 07:07
Re: goniometria
↑ kvaso:jak k tomu dospějeme, no, když si to představíš v té jednotkové kružnici, tak se vlastně otočíč o celý úhel pi (6pi/6) a ještě o jednu šestinu navíc, takže odchylka od osy x je stejná, jako při velikosti úhlu pi/6 jenom kosinus je tedy v záporných hodnotách.. A na velikost kosinu 30° přiješ třeba z rovnostranného trojúhelníku...
Neberme rozum do hrsti, mohli bychom zjistit, že je prázdná.
Offline

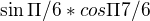 je jasné proč?
je jasné proč?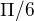 kludne byt, ak by si sem mohol dat postup bol by som rad
kludne byt, ak by si sem mohol dat postup bol by som rad