Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 06. 2013 12:24
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Gama/beta funkcia
Ahojte,
vedel by mi niekto poradiť, čo s týmto? Aspoň do akého tvaru to upraviť? Mám pred sebou aj papier so vzťahmi pre gama a beta funkcie, ale vôbec sa nechytám...
Prepísala som si súčin do tvaru:
Nič moc, ale na viac som sa nezmohla...
Offline
- (téma jako vyřešené označil(a) Blackflower)
#2 03. 06. 2013 13:33
Re: Gama/beta funkcia
↑ Blackflower:
Sice jsem to už dlouho neviděl, ale přijde mi že by v obou integrálech stačila substituce  . Pak tam dostaneš (dvakrát) přesně definici beta funkce v nějakých dvou bodech, to převedeš na gama funkce a doupravuješ. Vyšlo mi
. Pak tam dostaneš (dvakrát) přesně definici beta funkce v nějakých dvou bodech, to převedeš na gama funkce a doupravuješ. Vyšlo mi 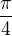 .
.
Offline
#3 03. 06. 2013 14:22 — Editoval Blackflower (03. 06. 2013 14:23)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Gama/beta funkcia
↑ LukasM: Mohlo by to byť takto?
Zatiaľ som sa ďalej nedostala, ale ešte porozmýšľam...
Offline
#4 03. 06. 2013 14:30
Re: Gama/beta funkcia
↑ Blackflower:
Mám to stejně. Teď si vzpomeň že  a potom se za chvíli ještě bude hodit
a potom se za chvíli ještě bude hodit  .
.
Offline
#5 03. 06. 2013 14:38
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Gama/beta funkcia
↑ LukasM: Vychádza mi  , lebo pred celým súčinom je ešte
, lebo pred celým súčinom je ešte 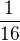 ... či to nemôžem násobiť?
... či to nemôžem násobiť?
Offline
#7 03. 06. 2013 14:54
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Gama/beta funkcia
↑ LukasM: Ja som strašné teliatko... už vidím, kde mám chybu. Ďakujem veľmi pekne za pomoc!
Offline

