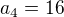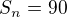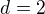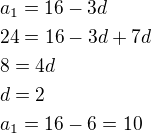Matematické Fórum

simanek · 14. 04. 2009 18:59

děkuji, jěště tu mam jednu ůlohu z finanční matematiky.

Automobil ztrácí hodnotu každý rok 15%
Určete dobu, kdy bude cena poloviční.

Cheop · 15. 04. 2009 07:28

↑ simanek:
$\left(0,85\right)^n=\frac 12\nln\cdot\log\,0,85=\log\left(\frac 12\right)\nln=-\frac{\log\,2}{\log\,0,85}\,\approx\,4,265\,\textrm{roku}$

simanek

prosim vás pěkně kde dělam chybu v tomto příkladu?

$a_4= 16$
$a_8= 24$
$S_n= 90$
$n=?$

$d=(Ar-As) : (r-s)$
$d=2$

$a1= a4-(3.d)$
$a1= 10$

$A_n = A_1 + (n-1).d$
$A_n = n+4$

$S_n=\frac{n}{2} (A_1+A_n )$

vyšla mi rovnice :

$n^2+14n-90=0$

výsledek má být 6, což mi nevychází, prosím o najití chyby. děkuji vám

gadgetka · 04. 05. 2009 20:35

$16=a_1+3d\nl24=a_1+7d\nl90=\frac{n}{2}(a_1+a_n)\nla_n=a_1+(n-1)\cdot d$

$a_1=16-3d\nl24=16-3d+7d\nl8=4d\nld=2\nla_1=16-6=10$

$90=\frac{n}{2}(10+a_n)\nla_n=10+2(n-1)\nl--------\nl180=10n+n\cdot a_n\nla_n=10+2n-2\nl-----------\nl180=10n+n(8+2n)\nl180=18n+2n^2\nln^2+9n-90=0\nln_{1,2}=\frac{-9\pm \sqrt{81+360}}{2}=\frac{-9\pm 21}{2}\nln_1=6\nln_2=-15$

taulik · 01. 06. 2009 21:15

jsem asi hloupá, prosím o radu
Mám spočítat součet ar. pst přičemž:
713+711+709+...+11+9+7

Vim, že vzorce jsou:
an=a1+(n-1)*d
sn=n/2*(a1+an)

No tak logicky a1=713 a d=-2 ale jak dál, to nějak nevím, prosím, pomůže mi někdo? Předem děkuju

gadgetka · 01. 06. 2009 22:05

$a_1=713\nld=-2\nla_n=7\nla_n=a_1+(n-1)\cdot d\nl7=713+(n-1)\cdot (-2)\nl7=713-2n+2\nl2n=708\nln=354\nls_n=\frac{n}{2}\cdot (a_1+a_n)\nls_{354}=\frac{354}{2}\cdot (713+7)=177\cdot 720=127440$

taulik · 01. 06. 2009 22:25

mě pořád nějak nešlo kde vemu to an, tak to bude u tohohle to poslední číslo, nebo je to jedno, jaký si zvolim z tý řady? jinak moc moc díky

Tom09 · 16. 01. 2013 15:10

Prosím o radu mám:
$a_{6}=-6$
$a_{2}+a_{5}=3$
$s_{7}=?$

((:-)) · 16. 01. 2013 16:23

↑ Tom09:

Založ si vlastnú tému, táto je už vyriešená...

Treba zapísať šiesty člen, druhý, piaty, vyriešiť sústavu (dostaneš a1,d) a zapísať vzťah pre súčet prvých 7 členov aritmetickej postupnosti s prvým členom a1 a diferenciou d.

petrik_ch · 16. 01. 2013 19:53

Ten priklad s radmi kina je pekny priklad na kvadraticku rovnicu, riesenie je aj tu:

http://www.hackmath.net/cz/priklad/592

Zaporny koren rovnice sa vyluci.

Kubajs6969 · 06. 06. 2013 13:35

Cheop napsal(a):
↑↑ Nikuskaska:
Jedná se o aritmetickou řadu, u které známe a_1, d, a S_n (přibližně)
Potřebujeme vypočítat n
$S_{n}=\frac n2\cdot(a_1+a_n)$
$a_n=a_1+(n-1)d$
$S_n=\frac n2(a_1+a_1+nd-d)\\1200=\frac n2(2\cdot 40+4n-4)\\1200=n(38+2n)\\2n^2+38n-1200=0\\n^2+19n-600=0$
Řešení této rovnice není celošíselné
Vyjde cca n = 16,75 řad.
Protože počet řad musí být celé číslo pak počet řad bude 17
Celkový počet sedadel bude 1224 a poslední řada bude mít 104 sedadel.

$a_{17}=40+16\cdot 4=104$
$S_n=\frac{17}{2}(40+104)\\S_n=72\cdot 17=1224$

PS: Kdyby těch řad bylo 16 pak by celkový počet sedadel bylo 1120 což je dál od 1200 než 1224

Můžu se zeptat jak ste dostal tenhle řádek ? 1200=n(38+2n)

Kubajs6969 · 06. 06. 2013 15:21

Cheop napsal(a):
↑↑ Nikuskaska:
Jedná se o aritmetickou řadu, u které známe a_1, d, a S_n (přibližně)
Potřebujeme vypočítat n
$S_{n}=\frac n2\cdot(a_1+a_n)$
$a_n=a_1+(n-1)d$
$S_n=\frac n2(a_1+a_1+nd-d)\\1200=\frac n2(2\cdot 40+4n-4)\\1200=n(38+2n)\\2n^2+38n-1200=0\\n^2+19n-600=0$
Řešení této rovnice není celošíselné
Vyjde cca n = 16,75 řad.
Protože počet řad musí být celé číslo pak počet řad bude 17
Celkový počet sedadel bude 1224 a poslední řada bude mít 104 sedadel.

$a_{17}=40+16\cdot 4=104$
$S_n=\frac{17}{2}(40+104)\\S_n=72\cdot 17=1224$

PS: Kdyby těch řad bylo 16 pak by celkový počet sedadel bylo 1120 což je dál od 1200 než 1224

není to 38n v předposledním řádku náhodou 22n ? mě to tak vyšlo a žádný 38 mi tam nevychází díky za vysvětlení;)

jelena · 06. 06. 2013 22:34

↑ Kubajs6969:

Zdravím,

není to 38n v předposledním řádku náhodou 22n ? mě to tak vyšlo a žádný 38 mi tam nevychází díky za vysvětlení;)

Ne, 38 plyne z úpravy rovnice
$S_n=\frac n2(a_1+a_1+nd-d)\\1200=\frac n2(2\cdot 40+4n-4)$

je rozumět přechodu z prvního řádku na druhý a následnému roznásobení závorek napravo? Děkuji. Jinak tato úloha je také zde (a více korektně by se mi jevilo nezapisovat rovnici, ale nerovnici $\frac n2(2\cdot 40+4n-4)\geq 1200$ (a zároveň $n \in \mathbb{N}$ ).

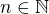Je lepší si založit nové téma s odkazem na již vyřešené, pokud ještě potřebuješ upřesnit řešení.

Matematické Fórum

#26 14. 04. 2009 18:59

Re: Aritmetická posloupnost příklad

#27 15. 04. 2009 07:28

Re: Aritmetická posloupnost příklad

#28 04. 05. 2009 20:15 — Editoval simanek (04. 05. 2009 20:16)

Re: Aritmetická posloupnost příklad

#29 04. 05. 2009 20:35

Re: Aritmetická posloupnost příklad

#30 01. 06. 2009 21:15

Re: Aritmetická posloupnost příklad

#31 01. 06. 2009 22:05

Re: Aritmetická posloupnost příklad

#32 01. 06. 2009 22:25

Re: Aritmetická posloupnost příklad

#33 16. 01. 2013 15:10

Re: Aritmetická posloupnost příklad

#34 16. 01. 2013 16:23

Re: Aritmetická posloupnost příklad

#35 16. 01. 2013 19:53

Re: Aritmetická posloupnost příklad

#36 06. 06. 2013 13:35

Re: Aritmetická posloupnost příklad

Cheop napsal(a):

#37 06. 06. 2013 15:21

Re: Aritmetická posloupnost příklad

Cheop napsal(a):

#38 06. 06. 2013 22:34

Re: Aritmetická posloupnost příklad

Zápatí