Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#3 09. 06. 2013 21:46 — Editoval cyrano52 (09. 06. 2013 21:56)
- cyrano52

- Místo: Frýdek-Místek
- Příspěvky: 705
- Škola: VŠB-TUO Ekonomická fakulta
- Pozice: student
- Reputace: 29
Re: diferenciální rovnice
↑ bismarck:
1. rovnice je lineární dif. rovnice 2. řádu s konstantními koeficienty a se speciální pravou stranou ve tvaru  . Řeší se následovně:
. Řeší se následovně:
Řešením této rovnice je součet tzv. obecného řešení zkr. nebo-li homogenní rovnice a odhadu některého partikulárního řešení dif. rovnice.
Nejprve je třeba si ji přepsat na homogenní rovnici (tedy rovnici s nulovou pravou stranou):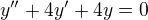
Nyní vytvoříme tzv. charakteristickou rovnici, kde jakoby "substituujeme" y za "k" a řád derivace za mocninu, tedy druhý řád --> druhá mocnina:
Spočítáme kořeny této kvadratické rovnice a sestavíme tzv. fundamentální systém řešení, který je složen ze dvou funkcí:
-pokud je diskriminant char. rovnice vetší než nula, tzn. máme 2 řešení, tak: a
a  , kde
, kde  jsou kořeny char. rovnice.
jsou kořeny char. rovnice.
-pokud je D=0: a
a  , kde
, kde 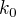 je dvojnásobný kořen.
je dvojnásobný kořen.
-pokud je D<0, máme tvar komplexního čísla ve tvaru 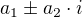 :
: a
a 
V našem případě máme D=0, tzn. máme dvojnásobný kořen  .
.
FSŘ: 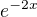 a
a 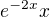
Obecné řešení té zkrácené (či homogenní) dif. rovnice je rovno lineární kombinaci daných funkcí, tzn.:
ypsilon se stříškou (nevím, jak to zde napsat :-)) = 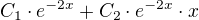
Dalším krokem je výpočet onoho odhadu některého partikulárního řešení dif. rovnice, které je obecně ve tvaru:
ypsilon s rovnou stříškou :-) = 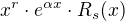 , kde r je násobnost kořene charakteristické rovnice jako čísla alfa v exponentu na pravé straně,
, kde r je násobnost kořene charakteristické rovnice jako čísla alfa v exponentu na pravé straně, 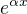 je identické s tou částí na pravé straně a "s" je stupeň mnohočlenu R.
je identické s tou částí na pravé straně a "s" je stupeň mnohočlenu R.
V našem případě je r=0 (protože alfa = 0, což není kořen char. rovnice), s=2 a dále  . Zapíšeme:
. Zapíšeme: 
Naším úkolem je zjistit hodnoty koeficientů A, B a C, což provedeme dosazením do původní rovnice. Abychom tak mohli učinit, je třeba nejprve spočítat 1. a 2. derivaci (z toho důvodu, že se v dif. rovnici vyskytují).:

Dosazení:
Použijeme metodu neurčitých koeficientů, tzn. poměřujeme koeficienty u stejných mocnin:
pro  :
: 

pro  :
: 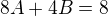

pro  :
: 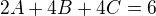
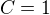
Tím odhadem je tedy: 
Obecné řešení diferenciální rovnice je tedy ve tvaru:
A je hotovo, doufám, že pomohlo trošku. :)
Největší bohatství je vzdělání - R. Kiyosaki
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)