Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 06. 2013 17:28 — Editoval cutrongxoay (09. 06. 2013 17:30)
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Vzajemna poloha primky a roviny
Zdravim
Urcete hodnoty parametru 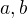 tak, aby primka
tak, aby primka ![kopírovat do textarea $p=[a-t;1+bt;2-2t]$](/mathtex/b1/b19b34d3046fc574a82cf13a4993c43e.gif) byla s rovinou
byla s rovinou 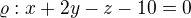
a) ruznobezna
b) lezela v rovine 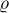
c) rovnobezna a nelezela v rovine 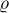
Mohli byste mi prosim ukazat, jak na to? Nejak to v tom nevidim. Uz v a) nevim, co mam udelat, vim maximalne, ze smernice by nemely byt stejne..
Diky
Offline
- (téma jako vyřešené označil(a) cutrongxoay)
#2 09. 06. 2013 19:43 — Editoval smajdalf (09. 06. 2013 19:47)
Re: Vzajemna poloha primky a roviny
Zdravím.
a) pokud má být přímka různoběžná s rovinou, vypadá to asi takto: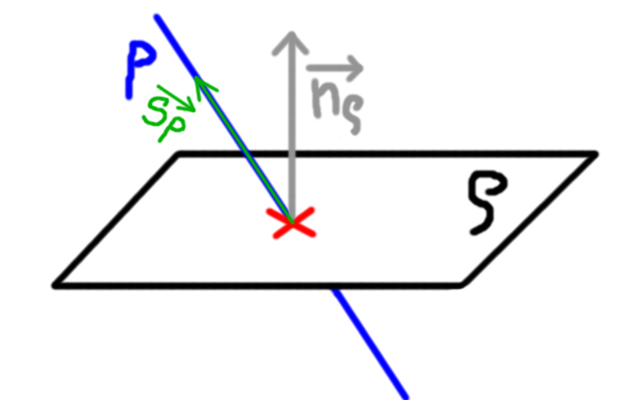
To znamená, že mají společný pouze jediný bod X.
A také to znamená, jak si říkal, že směrové vektory nesmí být lineárně závisle (tedy nesmí mít stejný směr).
Jinými slovy to znamená, že směrový vektor 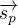 přímky a normálový vektor
přímky a normálový vektor 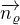 roviny nesmí být na sebe kolmé.
roviny nesmí být na sebe kolmé.
Pokud jsou dva vektory na sebe kolmé, pak jejich skalární součin je roven nule.
V našem případě tedy chceme, aby jeho hodnota byla různá od nuly.
Aspoň doufám, že tady nemelu blbiny :-D
Takže směrový vektor přímky je 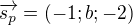 a normálový roviny
a normálový roviny 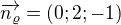 .
.
Skalární součin je: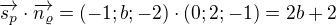
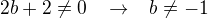 , jinak zapsáno
, jinak zapsáno 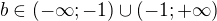 .
.
Parametr  dopočítáme tak, že parametrické rovnice přímky dosadíme do obecné rovnice roviny:
dopočítáme tak, že parametrické rovnice přímky dosadíme do obecné rovnice roviny: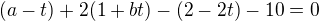
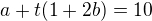 (1)
(1)
zvolíme t=0:
Tím jsme dostali bod přímky ![kopírovat do textarea $X=[10;1;2]$](/mathtex/6a/6a53100eb78b8d9da4292426ad06b955.gif)
Když ho dosadíme do rovnice roviny, vyjde 0=0, tedy tento bod zároveň leží jak na přímce p tak v rovině ρ.
Je tedy průsečíkem.
b) použiješ bod X a pak vektory 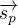 a
a 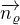 musí být na sebe kolmé (tedy skalární součin = 0). tedy a=10, b=-1.
musí být na sebe kolmé (tedy skalární součin = 0). tedy a=10, b=-1.
Aspoň doufám, že jsem na to šel správně, kdyžtak mě někdo prosím opravte.
"Znám dva tisíce způsobů jak nevyrobit žárovku,
potřeboval bych jeden, aby fungovala."
T. A. Edison
Offline
#3 09. 06. 2013 21:35 — Editoval cutrongxoay (09. 06. 2013 21:40)
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Vzajemna poloha primky a roviny
Docela jsem tomu porozumel, diky
Edit: vysledek pise, ze 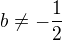 a
a 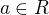
Offline
#4 10. 06. 2013 08:22
Re: Vzajemna poloha primky a roviny
↑ cutrongxoay:
Jo sakra, máš pravdu, jsem se asi překoukl:
Tady mám chybu 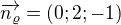 , ale má samozřejmě být
, ale má samozřejmě být 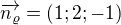 (jsou to koeficienty v obecné rovnici roviny:
(jsou to koeficienty v obecné rovnici roviny: 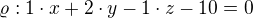 )
)
Takže potom ten skalární součin bude: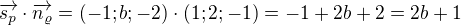
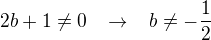
Promiň, hloupá chyba ;-/
"Znám dva tisíce způsobů jak nevyrobit žárovku,
potřeboval bych jeden, aby fungovala."
T. A. Edison
Offline
#5 10. 06. 2013 08:45
Re: Vzajemna poloha primky a roviny
↑ cutrongxoay:
A co se týče toho 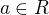 , to by mě asi nenapadlo, ale vlastně je to celkem logické, když se podíváš na rovnici té přímky
, to by mě asi nenapadlo, ale vlastně je to celkem logické, když se podíváš na rovnici té přímky 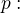

nebo se taky dá přepsat takto:![kopírovat do textarea $p: \;\; X=[a;1;2]+t \cdot (-1;b;-2)$](/mathtex/cb/cb9334556ef124e3521be807ef551265.gif) kde
kde![kopírovat do textarea $[a;1;2]$](/mathtex/c8/c8b36d7e5b6335177ae561dba307608d.gif) je bod určující přímku a
je bod určující přímku a 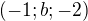 je její směrový vektor (tedy udává její směr).
je její směrový vektor (tedy udává její směr).
No a ten je přece nejdůležitější, když se jedná o vzájemnou polohu s jiným objektem.
Takže, když mají být různoběžné, tak jak název napovídá mají "běžet různými směry" a je jedno jaký bod na přímce si zvolím jako počáteční. To, že budou různoběžné závisí "jen" na vzájemné poloze směrového vektoru 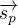 přímky a normálového vektoru
přímky a normálového vektoru 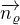 roviny.
roviny.
Tedy v našem případě může být 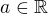 (jakékoliv).
(jakékoliv).
Pozn.: Jak se k tomuto výsledku dopracovat početně, nevím.
"Znám dva tisíce způsobů jak nevyrobit žárovku,
potřeboval bych jeden, aby fungovala."
T. A. Edison
Offline
#6 10. 06. 2013 18:09
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Vzajemna poloha primky a roviny
Ok, dekuji, taky by me mohlo napadnout, ze je chyba v tom normalovem vektoru, ale hlava nejak nemyslela.
Offline
