Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 06. 2013 19:51
geometrická posloupnost
Ahoj, mohu poprosit, jak mám postupovat k vyřešení této úlohy?
Hrany kvádru procházející jedním vrcholem tvoří geometrickou posloupnost, součet jejich délek je 7 cm. Povrch kvádru je  . Vypočítejte objem kvádru.
. Vypočítejte objem kvádru.

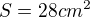
 ?
?
Offline
- (téma jako vyřešené označil(a) bonifax)
#2 11. 06. 2013 19:59
#4 11. 06. 2013 20:06 — Editoval bejf (11. 06. 2013 20:36)
Re: geometrická posloupnost
↑ bonifax:
První rovnici bych možná upravil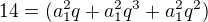

Ikdyž já si popravdě tím taky nejsem zcela jist. V takovém případě se omlouvám.
Offline
#5 11. 06. 2013 20:20 — Editoval bonifax (11. 06. 2013 20:20)
Re: geometrická posloupnost
↑ bejf:
dobře mno vpohodě,.)
V případě, že je to správný postup potom: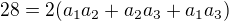
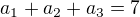
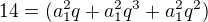
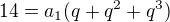
-------------------------------------

-------------------------------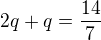

asi tak, nevím pravě jestli mohu dělit druhou rovnici první nebo jen první rovnici druhou..
Offline
#6 11. 06. 2013 20:21
Re: geometrická posloupnost
↑ bonifax:
Tam je to asi jedno, protože pořadí rovnic můžeš zaměňovat. Je to ekvivalentní úprava soustavy.
Offline
#9 11. 06. 2013 20:49
#10 11. 06. 2013 20:55 — Editoval bonifax (11. 06. 2013 21:02)
Re: geometrická posloupnost
↑ bejf:
tu pŕedchozí rovnicí v příspěvku 4 jsi pozměnil, příště se zmiň prosím, úplně jsem se ztratil.
Jinak ta druhá tvoje rovnice se mi nějak nezdá...
Vytkl jsi a_1q jenže první člen nemá q ne?
Myslím tato: 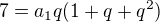 ?
?
původní rovnice byla 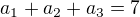


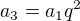
?
EDIT:
ps: jinak díky za odkaz
Offline
#11 11. 06. 2013 21:04 — Editoval bejf (11. 06. 2013 21:05)
Re: geometrická posloupnost
↑ bonifax:
Máš pravdu, moje chyba.
Správně podle mého posledního výpočtu má být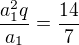
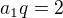 tedy
tedy  a
a 
Offline

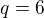
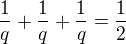
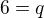

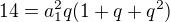


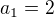

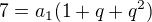
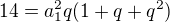

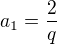
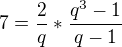

 a
a 