Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 01. 2009 14:58
derivace, fce
Nevim si rady s temito priklady, mohl by me nekdo navest, jakym zpusobem je spocist? diky
1. netusim vubec, uz jsme to tady nekde na foru resily, prolezl jsem i neco po netu, ale nejak stale nevim jak konkretne tento priklad vyresit.
2. zde me napadlo jen dosadit extremy x do fuknce y a zjistit tudiz hodnoty na y- min/max, ale zda se mi to moc jednoduche, takze pokud to je kravina, help pls
3. zname x,y. a hledame y=ax+b. Vim pouze ze a zjistime z prvni derivace a b dopocitame ze zadane funkce a pote primku ve tvaru y=ax+b zapiseme. Ale nejak nemuzu prijit na tu derivaci, je to spravny postup?
Offline
#2 11. 01. 2009 15:16 — Editoval gekoncik (11. 01. 2009 15:20)
Re: derivace, fce
Nevim jeslti je to dobre, ale u tech extremu provedes prvni derivaci. Vznikne ti kvadraticka funkce kterou polozis 0 (3x**2-6x+6). A me vyslo ze nema 0 koreny takze funkce je bud rostouci nebo klesajici po celem Df takze nema extremy.
Pokud by rovnice mela koreny pro = 0, tak provedes druho u derivaci a dosadis koreny do f''. Pokud
f''(x1) < 0 - max
f''(x2) > 0 - min
to ale nevim uz jiste ja to vetsinou urcuju z grafu :)
K te petce by mohlo stacit napsat:
cotg f'(0) = alfa
Kde f je funkce a 0 je iXová sousřadnice bodu.
Příspěvky od teoretiků mě na rozdíl od praktiků lehce iritují.
Offline
#3 11. 01. 2009 15:23 — Editoval Radek (11. 01. 2009 15:33)
Re: derivace, fce
gekoncik napsal(a):
Nevim jeslti je to dobre, ale u tech extremu provedes prvni derivaci. Vznikne ti kvadraticka funkce kterou polozis 0 (3x**2-6x+6). A me vyslo ze nema 0 koreny takze funkce je bud rostouci nebo klesajici po celem Df takze nema extremy.
Pokud by rovnice mela koreny pro = 0, tak provedes druho u derivaci a dosadis koreny do f''. Pokud
f''(x1) < 0 - max
f''(x2) > 0 - min
to ale nevim uz jiste ja to vetsinou urcuju z grafu :)
K te petce by mohlo stacit napsat:
cotg f'(0) = alfa
Kde f je funkce a 0 je iXová sousřadnice bodu.
Nemohu souhlasit, že by neměla extrémy, monotonní být může na celém definičním oboru. Tady se hledá extrém na uzavřeném intervalu a podle Weierstrassovy věty spojitá fce nabývá na uzavřeném int. maxima minima. Jinak řečeno dosaď krajní body intervalu.
ad5, ta derivace fce je 
Offline
#4 11. 01. 2009 16:01 — Editoval gekoncik (11. 01. 2009 16:02)
Re: derivace, fce
Radek: taky nemuzu souhlasit :)
Lokalni extremi se hledaji jsou v f'(x) = 0, a tuto podminku zadany interval splnuje. Pokud si zadas funkci do excelu nebo jineho programu vyjde ti rostouci funkce. Kdyztak koukni na:
http://user.mendelu.cz/marik/maw/index. … form=graft a zadej tam: ((((x^3)-(3*(x^2)))+(6*x))-2)
Příspěvky od teoretiků mě na rozdíl od praktiků lehce iritují.
Offline
#5 11. 01. 2009 16:26 — Editoval Radek (11. 01. 2009 16:27)
Re: derivace, fce
gekoncik napsal(a):
Radek: taky nemuzu souhlasit :)
Lokalni extremi se hledaji jsou v f'(x) = 0, a tuto podminku zadany interval splnuje. Pokud si zadas funkci do excelu nebo jineho programu vyjde ti rostouci funkce. Kdyztak koukni na:
http://user.mendelu.cz/marik/maw/index. … form=graft a zadej tam: ((((x^3)-(3*(x^2)))+(6*x))-2)
To máš pravdu. Vím jak ta fce vypadá :). Pokud hledáme globální extrémy na uzavřeném intervalu, pak hledáme extrémy lokální uvnitř tohoto intervalu. Postup jsi zadefinoval o pár postu výše a zjistil, že se nenachází žádný stacionární bod. Na uzavřeném intervalu musíme však vyšetřit ještě krajní body.
Offline
#7 11. 01. 2009 16:31
Re: derivace, fce
Tom napsal(a):
Takze preci jenom by ta 4. mela vychazet takto:
MAX:1,2)
MIN:(-1,-12)Radek napsal(a):
ad5, ta derivace fce je
diky, ale mohl bys to jeste dopocitat? nedari se mi stale ziskat a.
Jinak jeste potrebuju tu 1nicku:)
Tedy 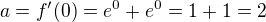
Offline