Matematické Fórum

Jewels · 12. 06. 2013 22:45

Zdravím, chtěl bych se zeptat jestli jsem postupoval správně.

$\lim_{x\to \infty} (\frac {x-3}{x+2})^{2x+1} = \lim_{x\to \infty} (\frac {x(1-\frac{3}{x})}{x(1+\frac{2}{x})})^{2x+1} = \lim_{x\to \infty} (\frac {1-\frac{3}{x}}{1+\frac{2}{x}})^{2x+1} = 1^\infty=1$

Hertas · 12. 06. 2013 22:54 — Editoval Hertas (12. 06. 2013 22:55)

mas to spatne, 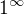$1^{\infty }$ je nedefinovany vyraz, musis si to prevest na exponencielu a dal vyuzit ze ze lim e^f(x)=e^lim f(x) takze $\lim_{x\to \infty }(\frac{x-3}{x+2})^{2x+1}=\lim_{x\to\infty }e^{(2x+1)ln(\frac{x-3}{x+2})}=e^{\lim_{x\to\infty }(2x+1)ln(\frac{x-3}{x+2})}$
nebo muzes pouzit heyneovu vetu a prevest si to na vypocet limity posloupnosti a snazit se to dostat do tvaru $\lim_{n\to \infty }(1+\frac{1}{p_{n}})^{p_{n}}$

Jewels · 12. 06. 2013 23:03

Tak to si nevím rady...Asi tak nějak chápu jak si dospěl k tomuto: $\lim_{x\to \infty }(\frac{x-3}{x+2})^{2x+1}=\lim_{x\to\infty }e^{(2x+1)ln(\frac{x-3}{x+2})}=e^{\lim_{x\to\infty }(2x+1)ln(\frac{x-3}{x+2})}$ ale nevim jak dal :(

Jewels · 12. 06. 2013 23:24

a nebo bych to ještě udělal takhle:

$\lim_{x\to \infty} (\frac {x-3}{x+2})^{2x+1} =\lim_{x\to \infty} (\frac {x+2-2-3}{x+2})^{2x+1} =\lim_{x\to \infty} (\frac {x+2}{x+2}+\frac {-5}{x+2})^{2x+1} =\lim_{x\to \infty} (1+\frac {-5}{x+2})^{2x+1}$

pak bych udělal substituci:
$\frac {-5}{x+2} = \frac {1}{z}$
$x=-5z-2$

a pokračoval v počítání limity:

$=\lim_{z\to \infty} (1+\frac {1}{z})^{2(-5z-2)+1} =\lim_{z\to \infty} (1+\frac {1}{z})^{-10z-3}$ $= \lim_{z\to \infty} [(1+\frac {1}{z})^{z}]^{-10} * (1+\frac {1}{z})^{-3}=e^{-10}$

Hertas · 12. 06. 2013 23:29

dobre tak ted pocitas limitu $\lim_{x\to\infty }(2x+1)ln(\frac{x-3}{x+2})$ upravis $\frac{x-3}{x+2}=1-\frac{5}{x+2}$ takze mas $\lim_{x\to\infty }(2x+1)ln(1-\frac{5}{x+2})$ ted tvoje $p_{x}=-\frac{x+2}{5}$ $\lim_{x\to\infty }(2x+1)ln(1-\frac{5}{x+2})^{\frac{\frac{x+2}{-5}}{\frac{x+2}{-5}}}=\lim_{x\to\infty }-5\frac{2x+1}{x+2}$