Matematické Fórum

Mar1ska · 17. 06. 2013 23:09

Ahoj, asi už jsem z toho jelen, ale nevím jak dál upravit tento na pohled jendoduchý zlomek. Opravdu stačí zkrátit první lomený výraz a to je celé? Zadání zní: $\frac{x^{3-}y^{3}}{x-y}-\frac{2xy}{x^{2}+xy+y^{2}}$
Já se dopočítala pouze k tomuto: $\frac{(x+y)^{2}}{x-y}-\frac{2xy}{x^{2}+xy+y^{2}}$

Blackflower · 17. 06. 2013 23:10

↑ Mar1ska: Ahoj,
uprav zlomky na spoločný menovateľ a využi tento vzťah: $(a^3-b^3)=(a-b)(a^2+ab+b^2)$

Mar1ska · 17. 06. 2013 23:10

↑ Mar1ska:↑↑ Hanis:

ok, tak když zkrátím x-y v prvním výrazu vznikne $\frac{x^{2}+xy +y^{2}}{x+y}-\frac{2xy}{x^{2}+xy+y^{2}}$

Tady mě taky už nic víc nenapadá..

Blackflower · 17. 06. 2013 23:13

↑ Mar1ska: Ja by som najprv upravila prvý zlomok:
$\frac{x^3-y^3}{x-y}=\frac{(x-y)(x^2+xy+y^2)}{x-y}=x^2+xy+y^2$

Mar1ska · 17. 06. 2013 23:17

↑ Blackflower:

↑ Blackflower:
ahaa. já to napsala s chybou..v zadání má být
$\frac{x^{3-}y^{3}}{x^{2}-y^{2}}-\frac{2xy}{x^{2}+xy+y^{2}}$

bejf · 17. 06. 2013 23:21

↑ Mar1ska:
Spíš takto:
$\frac{x^{3}-y^{3}}{x^{2}-y^{2}}-\frac{2xy}{x^{2}+xy+y^{2}}$

Blackflower · 17. 06. 2013 23:23

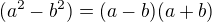↑ Mar1ska: Mne sa to hneď nezdalo :D vzorec na rozklad $(a^3-b^3)$ sa ti zíde tak či tak, ešte použiješ $(a^2-b^2)=(a-b)(a+b)$ , úprava na spoločného menovateľa a snáď to vyjde pekne. :)

Mar1ska · 17. 06. 2013 23:27

↑ Mar1ska:

právě ne:( Já jen potřebuju vědět, jestli už je $\frac{x^{2}+xy +y^{2}}{x+y}-\frac{2xy}{x^{2}+xy+y^{2}}$ výsledek..

Blackflower · 17. 06. 2013 23:30

↑ Mar1ska: Nemyslím si, že napríklad profesor by ti to pri opravovaní písomky uznal... ja si myslím, že to treba dať na spoločný menovateľ a upraviť.

Blackflower · 17. 06. 2013 23:34

Keď som to hodila do wolframu, vypľul mi toto: klik sem
Keby však bolo medzi zlomkami znamienko krát, výsledok vyzerá oveľa krajšie: klik sem

Mar1ska · 17. 06. 2013 23:48

↑ Blackflower:
už mi to vyšlo! Moc díky za postrkování ..:-)

Mar1ska · 17. 06. 2013 23:49

↑ Mar1ska:
x tam bohužel nebylo:-)

Blackflower

↑ Mar1ska: rado sa stalo :) tak to je divný príklad potom, lebo by sa to pekne vykrátilo :) no nič :D

Matematické Fórum

#1 17. 06. 2013 23:09

Upravy vyrazu

#2 17. 06. 2013 23:10

Re: Upravy vyrazu

#3 17. 06. 2013 23:10

Re: Upravy vyrazu

#4 17. 06. 2013 23:13

Re: Upravy vyrazu

#5 17. 06. 2013 23:13 Příspěvek uživatele Hanis byl skryt uživatelem Hanis. Důvod: zbytečně být tu 2

#6 17. 06. 2013 23:17

Re: Upravy vyrazu

#7 17. 06. 2013 23:21

Re: Upravy vyrazu

#8 17. 06. 2013 23:23

Re: Upravy vyrazu

#9 17. 06. 2013 23:27

Re: Upravy vyrazu

#10 17. 06. 2013 23:30

Re: Upravy vyrazu

#11 17. 06. 2013 23:34

Re: Upravy vyrazu

#12 17. 06. 2013 23:48

Re: Upravy vyrazu

#13 17. 06. 2013 23:49

Re: Upravy vyrazu

#14 17. 06. 2013 23:49 — Editoval Blackflower (17. 06. 2013 23:50)

Re: Upravy vyrazu

Zápatí