Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lokální a absolutní extrémy (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 06. 2013 23:04
Lokální a absolutní extrémy
Určete nejmenší a největší hodnotu funkce  na množině M určené podmínkou
na množině M určené podmínkou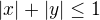 .
.
Dále ověřte zda-li má funkce f lokální extrémy.
Moc teda nerozumím co je myšleno nejmenší a největší hodnota funkce.
řešil jsem to:

z toho bod podezřelý z extrému ![kopírovat do textarea $[0,0]$](/mathtex/65/65b6edb92cc4ce515fc6a70a1d2d277d.gif)



pomocí sylvestrova kritéria (tuším), že  existuje extrém
existuje extrém lokální minimum v bodě
lokální minimum v bodě ![kopírovat do textarea $[0,0]$](/mathtex/65/65b6edb92cc4ce515fc6a70a1d2d277d.gif) .
.
tedka si nejsem jistej jak mám najíst absolutní extrémy.
obrazec bude vypadat nějak takhle (plus samozřejmě i vnitřek obrazce, ale nevím jak se ve wolframu zadává menší a rovná se Odkaz
hranice množiny budou tedy  ale nevím jak zjistit jestli tam mají absolutní maxima a minima.
ale nevím jak zjistit jestli tam mají absolutní maxima a minima.
pokud jsem tyto body dosadil do zadané funkce f vyšlo mi u každého bodu hodnota 1 což asi nebude správně.
Děkuji za návod řešení.
Jsou věci, které nikdy nepochopím.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 18. 06. 2013 12:07 — Editoval Rumburak (18. 06. 2013 13:44)
Re: Lokální a absolutní extrémy
Množina  je omezená a uzavřená, tedy kompaktní, funkce
je omezená a uzavřená, tedy kompaktní, funkce  je spojitá, takža absolutní extrémy funkce
je spojitá, takža absolutní extrémy funkce  na této množině existují.
na této množině existují.
Bod ![kopírovat do textarea $[0, 0]$](/mathtex/d7/d7a38e4440e6983b9695304b881867c6.gif) jako jediný kandidát na extrém uvnitř množiny
jako jediný kandidát na extrém uvnitř množiny  vyšel správně. To zmiňované kriterium si příliš nepamatuji (v zápise
vyšel správně. To zmiňované kriterium si příliš nepamatuji (v zápise
z přednášky mám u něj jako poznámku názor přednášejícího: "je to věta na nic"). Že v bodě ![kopírovat do textarea $[0, 0]$](/mathtex/d7/d7a38e4440e6983b9695304b881867c6.gif) a pouze v něm funkce nabývá
a pouze v něm funkce nabývá
absolutního minima lze zjistit takto:  ,
,  .
.
Zbývá vyšetřit situaci na hranici množiny  , tedy na množině určené rovnicí
, tedy na množině určené rovnicí  složené ze čtyř úseček vyjádřených rovnicemi
složené ze čtyř úseček vyjádřených rovnicemi  ,
,  ,
,  ,
,  ,
,
postupným dosazením do předpisu funkce  dostaneme čtyři funkce jedné proměnné
dostaneme čtyři funkce jedné proměnné  probíhající příslušné intervaly,
probíhající příslušné intervaly,
jejichž průběh vyšetříme metodami pro funkce jedné proměnné.
Offline
#4 18. 06. 2013 22:32 — Editoval Dopikasan (18. 06. 2013 22:38)
Re: Lokální a absolutní extrémy
↑ Bati:
↑ Rumburak:
nemužu si vzpomenout jak se dělají extrémy jedné proměnné :(
když to zderivuju vyjde mi všude 1 nebo -1 . to asi není správná cesta?
edit:
ve výsledkách je Absolutní maximum: [0;-1]; [0; 1]; [-1; 0]; [1; 0]
Absolutní minimum (i lokální): [0; 0]
Díky za objasnění postupu
Jsou věci, které nikdy nepochopím.
Offline
#5 18. 06. 2013 22:36
#7 18. 06. 2013 22:50
#12 19. 06. 2013 14:10
Re: Lokální a absolutní extrémy
↑ Bati:
na střední jsme to nebrali.
můj postup: zderivoval jsem to a položil rovno nule tedy:  z toho jsou kořeny
z toho jsou kořeny 
tedka budu dosazovat do první derivace abych zjistil jestli klesá nebo roste.
-2= roste
0=klesá
2=roste
takže extrém je v bodě -1?
moc tomu nerozumím, kdyby ses prosím rozepsal :)
Jsou věci, které nikdy nepochopím.
Offline
#16 20. 06. 2013 09:20 — Editoval Rumburak (20. 06. 2013 09:22)
Re: Lokální a absolutní extrémy
↑ Dopikasan:
Když hledáme extrém funkce jedné proměnné na uzavřeném intervalu, pak "podezřelými" budou
(1) body, v nichž derivace je rovna 0 nebo neexistuje,
(2) krajní body intervalu (o tom se kolega ↑ Bati: patrně opomněl zmínit).
Jestliže hledáme pouze absolutní extrémy, pak stačí v podezřelých bodech porovnat jejich funkční hodnoty,
takže např. v podezřelém bodě s nejmenší funkční hodnotou bude absolutní minimum na této množině.
Obdobně když takových intervalů máme více, jako v našem případě.
Offline
#17 20. 06. 2013 12:59
Re: Lokální a absolutní extrémy
↑ Rumburak:
↑ Dopikasan:
možná tomu rozumím už, jen pro kontrolu na intervalu 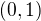 první derivace která je
první derivace která je  zvolim
zvolim  kterou dosadím do prnví derivace abych zjistil jestli tam je lokální max nebo min.
kterou dosadím do prnví derivace abych zjistil jestli tam je lokální max nebo min.
vyjde mi to  což je rozhodně záporné takže tam je lokální maximum?
což je rozhodně záporné takže tam je lokální maximum?
stejně udělám všechny další 3 body které jsou podezřelé z extremu ?
Jsou věci, které nikdy nepochopím.
Offline
#18 20. 06. 2013 17:11
Re: Lokální a absolutní extrémy
↑ Dopikasan:
Abychom si rozuměli, shrňme fakta.
Množina určená nerovnicí 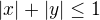 je čtverec s vrcholy
je čtverec s vrcholy ![kopírovat do textarea $A[1, 0], B[0, 1], C[-1, 0], D[0, -1]$](/mathtex/b6/b6669815a3aad23aa242c7b022247992.gif) (doporučuji nakreslit).
(doporučuji nakreslit).
Vezměme třeba stranu  , která je vyjádřena rovnicí
, která je vyjádřena rovnicí  . (Každý bod této úsečky je takto jednoznačně určen
. (Každý bod této úsečky je takto jednoznačně určen
svojí x-ovou souřadnicí, např. bod  získáme volbou
získáme volbou 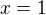 , bod
, bod  volbou
volbou  .) Funkce
.) Funkce 
má na této úsečce tvar
 .
.
Položíme-li tedy  , pak vyšetřít průběh funkce
, pak vyšetřít průběh funkce  na úsečce
na úsečce  je de facto totéž jako
je de facto totéž jako
vyšetřit průběh funkce  na intervalu
na intervalu  . Takto budeme nyní postupovat.
. Takto budeme nyní postupovat.
K bodům podezřelým na extrém funkce  na intervalu
na intervalu  nutno zařadit jeho krajní body, tedy body
nutno zařadit jeho krajní body, tedy body  a
a  .
.
Uvnitř uvedeného untervalu budeme dále hledat body, v nichž 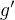 buťto neexistuje nebo je rovna 0 . První z těchto podmínek nám zde žádný
buťto neexistuje nebo je rovna 0 . První z těchto podmínek nám zde žádný
podezřelý bod nedá, protože funkce  má derivaci v každém bodě, a sice
má derivaci v každém bodě, a sice  . Druhá z podmínek, tj.
. Druhá z podmínek, tj.  , vede
, vede
k rovnici  , jejíž řešení
, jejíž řešení 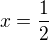 patří do intervalu
patří do intervalu  .
.
Veškeré body, v nichž by funkce  mohla mít na intervalu
mohla mít na intervalu  extrém, jsou tedy
extrém, jsou tedy  , jimž odpovídají body
, jimž odpovídají body ![kopírovat do textarea $B, A, \[\frac{1}{2} , \frac{1}{2}\]$](/mathtex/cb/cb27e93e1243bdf80a383c64f0ab2d88.gif)
úsečky  .
.
Obdobně bychom na zbývajících stranách čtverce našli zbývající kandidáty pro extrémy funkce  na HRANICI uzavřeného čtverci
na HRANICI uzavřeného čtverci 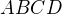 .
.
Když k nim přidáme vnitřní bod ![kopírovat do textarea $[0 , 0]$](/mathtex/8a/8a95ac00d1f83a25784491feb1714dd7.gif) zařazený mezi kandidáty na extrém PŘES CELÝ ČTVEREC již dříve, bude množina všech těchto kandidátů
zařazený mezi kandidáty na extrém PŘES CELÝ ČTVEREC již dříve, bude množina všech těchto kandidátů
kompletní. Označme ji  .
.
Pokud by nás zajímaly i všechny lokální extrémy, museli bychom v okolí každého bodu množiny  vyšetřit chování funkce
vyšetřit chování funkce  . Když hledáme pouze
. Když hledáme pouze
absolutní extrémy (o nichž v tomto případě víme, že existují), stačí spočíst hodnoty  a najít mezi nimi největší a nejmenší.
a najít mezi nimi největší a nejmenší.
POZNÁMKA. Zda funkce  jedné proměnné nabývá lokálního extrému v bodě
jedné proměnné nabývá lokálního extrému v bodě  , kde
, kde  , se dá (často) poznat podle hodnoty
, se dá (často) poznat podle hodnoty 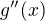 ,
,
pokud existuje. Kladná hodnota dává lokální minimum, záporná lokální maximum. Ale u funkcí více proměnných je situace o dost složitější.
Offline
#19 20. 06. 2013 23:49
Re: Lokální a absolutní extrémy
↑ Rumburak:
díky za podrobný vysvětlení, je mi vše jasné kromě toho jestli teda v bodě  je absolutní extrém nebo ne?
je absolutní extrém nebo ne?
pokud do rovnice  dosadim polovinu intervalu
dosadim polovinu intervalu  což je
což je  vyjde mi nula takže nevím jeslti tam je maximum nebo minimum?
vyjde mi nula takže nevím jeslti tam je maximum nebo minimum?
Jsou věci, které nikdy nepochopím.
Offline
#20 21. 06. 2013 09:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lokální a absolutní extrémy
Zdravím v tématu,
↑ Dopikasan:
pana Fiňka bys měl jednou přečíst :-) Schválně, kde o tom pojednává?
K poslednímu příspěvku ↑ 19:. Výraz  je zápis 1. derivace, tedy pokud do tohoto zápisu dosazuješ
je zápis 1. derivace, tedy pokud do tohoto zápisu dosazuješ  , což je jeho nulový bod, tak hodnota výrazu je 0 (jak jinak). Pokud chceš ověřit kvalitu extrému v bodě
, což je jeho nulový bod, tak hodnota výrazu je 0 (jak jinak). Pokud chceš ověřit kvalitu extrému v bodě 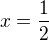 , potom musíš ověřovat znaménko 1. derivace před a po tomto bodu, ale pořád na intervalu od 0 do 1. Tedy např. před je
, potom musíš ověřovat znaménko 1. derivace před a po tomto bodu, ale pořád na intervalu od 0 do 1. Tedy např. před je 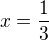 , po je
, po je  . Jak tedy dopadl bod
. Jak tedy dopadl bod 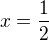 ?
?
Pro ověření, zda na hranici intervalu je maximum nebo minimum, stačí "hraniční x" dosazovat do předpisu funkce a porovnat funkční hodnoty. Proč nepoužiješ hodnotu před nebo po hraniční intervalu? Protože již jedna z nich na intervalu není a Tebe nezajímá, že soused má větší švestky (porovnáváš jen své švestky rostoucí u plotů, u sloupků plotů v rozích a uprostřed zahrady).
Tedy na intervalu  do předpisu funkce
do předpisu funkce  dosazuješ postupně
dosazuješ postupně  ,
, 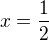 ,
,  . Jak to dopadlo u jednotlivých hodnot funkce? Děkuji.
. Jak to dopadlo u jednotlivých hodnot funkce? Děkuji.
Offline
#21 21. 06. 2013 10:49
Re: Lokální a absolutní extrémy
↑ jelena:
aha, já to dosazoval do první derivace :X
takže já si vyjádřím předpis funkce  kam dosadím body z intervalu
kam dosadím body z intervalu 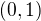 ?
?
pokud funkční hodnota je největší na krajích intervalu tedy v nule nebo jedničce je to globální extrém? pokud uvnitř intervalu je to jak lokální tak globální extrém?
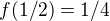
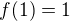
jelikož jsou největší hodnoty na krajích intervalu jedná se o globální(absolutní) maximum?
pana Fiňka bys měl jednou přečíst :-) Schválně, kde o tom pojednává?
Teorie v jeho scriptech je pro mě místy dost nejasná a je tam málo ukázkových příkladů na kterých je to ukázané.
Jsou věci, které nikdy nepochopím.
Offline
#22 21. 06. 2013 11:46 — Editoval Rumburak (21. 06. 2013 11:50)
Re: Lokální a absolutní extrémy
↑ Dopikasan:
Ten interval je zde vhodné brát jako uzavřený. Dále je třeba psát ,
,  ,
, 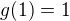
(funkce  je funkcí dvou proměnných) - takovéto chyby, zvláště jsou-li notoricky opakovány, mohou být příčinou vyhazovu od zkoušky.
je funkcí dvou proměnných) - takovéto chyby, zvláště jsou-li notoricky opakovány, mohou být příčinou vyhazovu od zkoušky.
Výsledky uvedených výpočtů můžeme vyhodnotit třeba takto:
Funkce  je spojitá na uzavřeném interval
je spojitá na uzavřeném interval  , což je kompaktní množina, takže existují body
, což je kompaktní množina, takže existují body 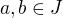 takové , že
takové , že
 .
.
Body  nutno hledat v množině
nutno hledat v množině  sestavené z bodů podezřelých na extrém, tj. z krajních bodů jntervalu
sestavené z bodů podezřelých na extrém, tj. z krajních bodů jntervalu  ,
,
z bodů, kde  a z bodů, kde
a z bodů, kde  neexituje (takové body zde ale nejsou) .
neexituje (takové body zde ale nejsou) .
Porovnáním funkčních hodnot máme  , pro bod
, pro bod  dostáváme 2 řešení:
dostáváme 2 řešení:  . Jde o extrémy absolutní
. Jde o extrémy absolutní
(neboli extrémy globální) funkce  na množině
na množině  a bylo-li jich dosaženo na hranici této množiny či ne, není to pro jejich kvalifikaci
a bylo-li jich dosaženo na hranici této množiny či ne, není to pro jejich kvalifikaci
nijak podstatné). Každý z nich je samozřejmě i extrémem lokálním , při čemž žádné další lokální extrémy neexistují (stále ještě hovoříme
pouze o extrémecch funkce  na množině
na množině  ) .
) .
Dokud toto nebude pochopeno bezezbytku, nemá smysl pouštět se dál. Doporučuji pečlivě si prostudovat teorii včetně definic oněch pojmů.
Offline
#23 21. 06. 2013 11:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lokální a absolutní extrémy
↑ Dopikasan:
takové drobnosti: kam dosadím krajní body intervalu  (závorka musí být uzavřená, ne okrouhlá).
(závorka musí být uzavřená, ne okrouhlá).
Ještě pro pořádek - abychom neztratili, že vyšetřujeme funkci  , tak po nalezení
, tak po nalezení  ,
, 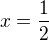 ,
,  a k nim odpovídajících hodnot y dosazujeme x a y do předpisu zadané funkce, jelikož v důsledku budeme posuzovat hodnotu funkce na všech bodech, co jsme našli i na lokálním extrému uvnitř množiny:
a k nim odpovídajících hodnot y dosazujeme x a y do předpisu zadané funkce, jelikož v důsledku budeme posuzovat hodnotu funkce na všech bodech, co jsme našli i na lokálním extrému uvnitř množiny: ![kopírovat do textarea $[0,0]$](/mathtex/65/65b6edb92cc4ce515fc6a70a1d2d277d.gif) . Také celkem máme došetřit každou stranu čtverce - ale to už myslím bylo řečeno.
. Také celkem máme došetřit každou stranu čtverce - ale to už myslím bylo řečeno.
Toto se mi zdá přehledné dost a hodnocení extrému jsi provedl ve stejném smyslu, jako v odkazu.
Teď z náhledu vidím kolegu Rumburaka, zdravím, děkuji a příspěvek ponechám jen pro seznámení s materiály učitele pana kolegy, zda jsou opravu tak nepřehledné. Omluva za vstup.
Offline
#24 21. 06. 2013 15:07
Re: Lokální a absolutní extrémy
↑ Rumburak:
moc se omlouvám, že jsem tak strašně moc hloupej, ale jak tedy určím jestli ten extrém je absolutní maximum nebo minimum? když funkční hodnoty 

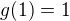 jsou kladné tak má být absolutní minimum?
jsou kladné tak má být absolutní minimum?
Jsou věci, které nikdy nepochopím.
Offline
#25 21. 06. 2013 16:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lokální a absolutní extrémy
Dopikasan napsal(a):
když funkční hodnoty


jsou kladné tak má být absolutní minimum?
Když funkční hodnoty jsou kladné, tak jsou kladné. Z tohoto faktu žádný závěr o maximumu nebo minimu neuděláš. V tomto kroku již porovnáváš přímo hodnoty funkce - která je z hodnot největší, nejmenší? Zde vidíme, že  a
a 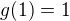 mají stejnou hodnotu (1) a žádná hodnota funkce na tomto intervalu není větší. je tedy splněna DEFINICE 6.30 (p. Finěk).
mají stejnou hodnotu (1) a žádná hodnota funkce na tomto intervalu není větší. je tedy splněna DEFINICE 6.30 (p. Finěk).
Naopak  je nejmenší hodnota na intervalu (navíc pomocí změny znamének 1. derivace jsme prokázali, že přechodem přes tento bod 1. derivace změní znaménko z (-) na (+), tedy to bylo lokální minimum. Je to zároveň i absolutní minimum na intervalu. Je splněna DEFINICE 6.32 (p. Finěk).
je nejmenší hodnota na intervalu (navíc pomocí změny znamének 1. derivace jsme prokázali, že přechodem přes tento bod 1. derivace změní znaménko z (-) na (+), tedy to bylo lokální minimum. Je to zároveň i absolutní minimum na intervalu. Je splněna DEFINICE 6.32 (p. Finěk).
Ovšem tak jsme vyšetřili pouze úsečku čtverce pro x na intervalu  . Nesmíme zapomenout dovyšetřit další úsečky (opět opakuji, bylo doporučeno usnadnění) a hodnotu funkce
. Nesmíme zapomenout dovyšetřit další úsečky (opět opakuji, bylo doporučeno usnadnění) a hodnotu funkce  v bodě
v bodě ![kopírovat do textarea $[0,0]$](/mathtex/65/65b6edb92cc4ce515fc6a70a1d2d277d.gif) . Potom je nejlepší si sestavit tabulku hodnot funkce
. Potom je nejlepší si sestavit tabulku hodnot funkce  pro každý podezřelý bod, co byl vyšetřován a zkontrolovat, že jsme nevynechali nic (vnitřní oblast, hranici (čtverec), vrcholy čtverce).
pro každý podezřelý bod, co byl vyšetřován a zkontrolovat, že jsme nevynechali nic (vnitřní oblast, hranici (čtverec), vrcholy čtverce).
OT: pro kolegu Rumburaka: Pan Finěk - TUL - Liberec - Ještěd - doplň závěrečnou asociaci, prosím :-)
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lokální a absolutní extrémy (TOTO TÉMA JE VYŘEŠENÉ)

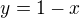 nebo
nebo  ,
, ![kopírovat do textarea $x\in[0,1]$](/mathtex/a3/a35805693e94e4f44290ccd56f46ee4a.gif) , neboť pro f platí
, neboť pro f platí  a
a  .
.
