Matematické Fórum

Zdravím

Jelikož na téma nikdo nereaguje takto zkusím.

Zaprvé vůbec si nejsem jistý, jak je celá úloha myšlena po technické stránce, kdyby byl přiložen náčrtek, dost by to situaci zjednodušilo. Je to třeba už jen kvůli tomu, zdali se píst pohybuje vodorovně či svisle...

"Mám tlakovou nádobu s dostatečným přebytkem tlaku - cca 300 atm. dále regulační ventil, který udržuje konstantní úroveň tlaku 120 atm"

Chápu tedy, že v nádobě mám plyn o tomto tlaku, po otevření ventilu se tlak adiabaticky sníží na 120?
Dále pro jistotu vysvětlit co přesně se myslí pojmem světlost.


Tedy rád pomůžu pokud mi bude nějak přiblíženo zadání, úloha se zatím nejeví jako až moc komplikovaná. (ale kdo ví?)
Děkuji

Zdravím
Tak ještě poslední dotaz, neboť úloha v té podobě jak sem jí pochopil nemá se zadanýma hodnotama řešení - chybí počáteční objem (resp není zadaná velikost modré nádoby)

1. Mám modrou nádobu, neznámý objem, vim co je v ní za plyn (při řešení je důležité vědět jestli se jedná o jednoatomový plyn nebo dvouatomový...), znám počáteční tlak - 300*atmosférickýtlak

2. Nádoba se otevře - plyn se začne roztahovat, tlak plynu tedy musí klesat. Všechno probíhá bez tepelných výměn (adiabaticky)


3. Plyn se roztahuje do roury, jejíž délku ani šířku neznám přesně, snažim se najít jejich ideální kombinaci viz dále

4. Plyn před sebou tlačí píst o hmotnosti m (kolik tedy váží?) a tlačí ho tak dlouho, dokud nebude mít takovou rychlost, aby jeho energie byla 100J

5. V tuto chvíli mě zajímá tlak plynu a jak dlouho to trvalo

Je to tak?? Jestliže ano, pak nám vadí právě to, že neznáme ten počáteční objem. Pokud ho lze považovat za tak velký, že se hodnota tlaku po celou dobu nemění, tak se úloha stává takřka primitivní.

Prosím tedy o upřesnění, pokud je úloha opravdu myšlena takto, tak sem připíšu k čemu sem se dopracoval (i když to není úplně výsledek)
Děkuji

Zdravím
Za předpokladu konstantního tlaku se úloha velice zjednoduššuje.
Napřed zjistíme, jaká síla působí na píst.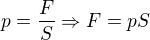



Kde S je plocha pístu. Vidíme, že síla se s časem nemění.
Teď se pokusíme popsat pohyb pístu. Newtonův zákon dává: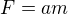



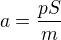
Vidíme že i zrychlení je konstantní
Dále tedy platí: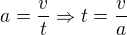


Jelikož tlak, hmotnost a koncová rychlost jsou pevně zadaná čísla, musíme volit plochu pístu co největší.
Tedy pokud by neexistovalo omezení pro délku válce, zvolili bychom průměr co největší.

Teď se pokusíme najít nějaký vzah, který nám dává do souvislosti plochu a délku válce.
Jelikož je zrychlení konstantní platí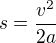


Kde s můžeme považovat za délku válce, tudíž písmeno "v" značí koncovou rychlost. Dosazením za "a":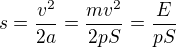


Po úpravě: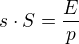


Další postup je myslím zřejmý:
1. Zvolíme největší možný průměr, dosadíme do poslední rovnice a určíme délku válce. Pokud se délka válce pohybuje v dovoleném rozmezí, přeskočíme bod (2). Pokud by délka vycházela větší než je dovoleno, úloha nemá řešení. Pokud vyjde kratší tak...
(2) ... vezmeme co nejkratší možnou délku válce a dosadíme do poslední rovnice a zjistíme plochu S (tedy i průměr).

3. Vypočítáme koncovou rychlost v.
4. Dosadíme do rovnice pro čas. - ˇuloha je vyřešená



Pro úplnost



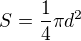
Je vše jasné a vychází to??

Dobrý den

2) Jestliže je láhev plynu dostatečně velká, lze za konstantní považovat jakýkoli tlak, tudíž volíme co největší možný.

4) Vyrážím do válce, neovlivňuji píst - vzduch píst začne ovlivňovat okamžitě, neboť píst se nepohybuje z toho důvodu, že v něm i mimo něj je tlak stejný (a to atmosferický). Ale jakmile tam začne proudit vzduch, tak tlak vzroste prakticky okamžitě. Sice nevzroste na danou hodnotu okamžitě, ale postupně, nic méně píst se začne pohybovat hned.

5) Zde již klesá můj tlak - To je nejspíš pravda tento faktor sem nezapočítával, neboť sem si situaci představoval trochu jinak (špatně :) )

6) Pakliže klade ze začátku nějaký odpor, je potřeba tento odpor nějak přesněji popsat, nic méně to musí být součást zadání, neboť v ideálním modelu situace píst žádný odpor klást nebude.

7) Ano tlak teoreticky trošku poklesne, nicméně jelikož se jedná o milimetry, bude tato změna nepatrná (tlak se vyrovná téměř okamžitě). To že se píst bude pohybovat taky nezpůsobí pokles tlaku, neboť pohyb pístu je snaha tlaky vyrovnávat.

Celou situaci tam komplikuje právě ten časový úsek těsně po otevření ventilu. Zkusím něco najít o šíření tlaku v plynech a situaci zkusím přehodnotit.

Dále by mě zajímalo jak jste k takové úloze přišel? Pokud se jedná jen o praktické využití tak bych se spíše přiklonil k experimentálnímu určení ideálních rozměrů.