Matematické Fórum

OndraVesely

AAhoj, mohli byste mi poradit s timto integralem?

$\int_{0}^{\pi /2}sin^{n}x\cdot dx$

Moje reseni:
1. Predpokladam ze n>=1
2. Vyresil jsem integral pro n=1
3. Vyresil jsem integral pro n=2
4. Dokazal jsem ze pro n>2 plati tento vzorec: $\int_{}^{}sin^{n}(ax)dx=-\frac{sin^{n-1}(ax)\cdot cos(ax)}{n\cdot a}+\frac{n-1}{n}\int_{}^{}sin^{n-2}(ax)dx$ .
Muj problem spociva v tom ze si nejsem jisty zdali plati i toto: $\int_{0}^{\pi /2}sin^{n}(ax)dx=-\frac{sin^{n-1}(ax)\cdot cos(ax)}{n\cdot a}+\frac{n-1}{n}\int_{0}^{\pi /2}sin^{n-2}(ax)dx$ .
Pokud by tento vzorec platil pak by pro mne byl problem vyresit ten integral $\int_{0}^{\pi /2}sin^{n-2}(ax)dx$ . Myslím že ani není řešitelný - potom bude tedy konečným výsledkem asi tento vzorec že ano: $\int_{0}^{\pi /2}sin^{n}(ax)dx=-\frac{sin^{n-1}(ax)\cdot cos(ax)}{n\cdot a}+\frac{n-1}{n}\int_{0}^{\pi /2}sin^{n-2}(ax)dx$ ?

Diky predem

martisek · 23. 06. 2013 22:24

↑ OndraVesely:

Ahoj,

1. Pro lichou mocninu je

$\int_0^{\pi /2}sin^{2n+1}x\cdot dx = \int_0^{\pi /2}sinx\cdot sin^{2n}x\cdot dx=\int_0^{\pi /2}sinx\cdot (1-cos^2x) ^n\cdot dx$

a substituce cos x = t

2. Pro sudou mocninu

$\int_0^{\pi /2}sin^{2n}x\cdot dx = \int_0^{\pi /2}\left( \frac {1-cos 2x} 2\right)^n dx$

a podle toho, zda je n liché nebo sudé postupujeme dále dle 1, anebo 2

Jj · 24. 06. 2013 00:05

↑ OndraVesely:

Už jen pro zajímavost uvádím po nahlédnutí do tabulky
určitých integrálů v "Rektorysovi":

$\int_0^{\pi /2}sin^{2n}x\cdot dx = \int_0^{\pi /2}cos^{2n}x\cdot dx = \frac{1\cdot 3\cdot 5\cdot \ldots \cdot (2n-1)}{2\cdot 4\cdot 6 \cdot \ldots \cdot 2n}\frac{\pi}{2}$

$\int_0^{\pi /2}sin^{2n+1}x\cdot dx = \int_0^{\pi /2}cos^{2n+1}x\cdot dx = \frac{2\cdot 4\cdot 6\cdot \ldots \cdot 2n}{1\cdot 3\cdot 5\cdot \ldots \cdot (2n+1)}\frac{\pi}{2}$

Obecný integrál uvedený na začátku Vašem dotazu jste vyřešil správně (i když bude zřejmě lepší v praxi uplatnit postup kolegy Martiska).

OndraVesely

↑ Jj:
Myslim že to co jste napsal je správné řešení ale bohužel nevím jak se k tomu dostat. Myslím že se podobné příklady řeší tak, že si napíšeme $\int_{0}^{\pi /2}sin^{n}x\cdot dx=I_n$

tedy:

$\frac {d}{dx}(\cos x\sin^{n-1}x)=-\sin^n x+(n-1)\cos^2x\sin^{n-2}x= -\sin^n x+(n-1)(1-\sin^2x)\sin^{n-2}x$
$=-n\sin^nx+(n-1)sin^{n-2}x$

tzn.:

$\frac {d}{dx}(\cos x\sin^{n-1}x)=-n\sin^nx+(n-1)sin^{n-2}x$

zintegrujeme rovnici:

$\cos x\sin^{n-1}x=0=-n\int_{}^{}sin^nx+(n-1)\int_{}^{}sin^{n-2}x$

Pak:

$0=-n\cdot I_n+(n-1)\cdot I_{n-2}$

tzn.:

$I_n= \frac{(n-1) }{n}\cdot I_{n-2}$

Vidíte, neumím se dostat k těm vašim vzorcům:
$\int_0^{\pi /2}sin^{2n}x\cdot dx = \int_0^{\pi /2}cos^{2n}x\cdot dx = \frac{1\cdot 3\cdot 5\cdot \ldots \cdot (2n-1)}{2\cdot 4\cdot 6 \cdot \ldots \cdot 2n}\frac{\pi}{2}$
a
$\int_0^{\pi /2}sin^{2n+1}x\cdot dx = \int_0^{\pi /2}cos^{2n+1}x\cdot dx = \frac{2\cdot 4\cdot 6\cdot \ldots \cdot 2n}{1\cdot 3\cdot 5\cdot \ldots \cdot (2n+1)}\frac{\pi}{2}$

Můžete mi prosím pomoct?

Respektive mezi vaším řešením a mým řešením je jistá podobnost předpokládám že:
pro 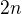$2n$ je $\frac{1\cdot 3\cdot 5\cdot \ldots }{2\cdot 4\cdot 6\cdot \ldots }\cdot \frac{\pi }{2}=I_{2n-2}$ a pro $2n+1$ je $\frac{2\cdot 4\cdot 6\cdot \ldots }{1\cdot 3\cdot 5\cdot \ldots }\cdot \frac{\pi }{2}=I_{2n-1}$ . Proč tomu tak je a jak se na to přišlo, to nevím.

OndraVesely · 24. 06. 2013 17:51

↑ martisek:Vaše řešení jsem zkoušel a došel jsem v obou případech tam kde se musel vyřešit integrál s tou mocninou. Po substitucích vám tam ty mocniny na n-tou stejně zůstanou a pak bych asi musel využít binomickou větu. Bouhužel jsem na použítí těchto složitějších triků levý.

Matematické Fórum

#1 23. 06. 2013 18:24 — Editoval OndraVesely (23. 06. 2013 18:56)

Integral

#2 23. 06. 2013 22:24

Re: Integral

#3 24. 06. 2013 00:05

Re: Integral

#4 24. 06. 2013 17:43 — Editoval OndraVesely (24. 06. 2013 18:20)

Re: Integral

#5 24. 06. 2013 17:51

Re: Integral

Zápatí