Matematické Fórum

bentrix · 11. 01. 2009 18:10

ahoj prosim vas pomuze mi nekdo s toutou funkci?? graf vim, vim ze je suda ale potreboval bych vyresit stac. body, inflexní body, pruseciky s osou, a asymptoty bez a se směrnicí . byl byste nekdo ochoten mi pomoct , predem dekuju

halogan · 11. 01. 2009 18:15

A jak jsi udělal graf bez těch informací? Že by počítač?

1) asymptota bez smernice: spocitej si limitu v bode nespojitosti (zprava a zleva). Pokud bude nevlastni, tak tam mas asymptotu
2) asymptota se směrnicí, na to máš vzorce. k = lim f(x)/x, do nekonecna; q = lim (f(x) - kx), do nekonecna; y = kx + q
3) stac. body - máš první derivaci?
4) inflexe - máš druhou derivaci?
5) průsečíky s osou - s osou y to nemá průsečík (víš proč?) s osou x v bodě [-2; 0], víš proč?

kaja.marik · 11. 01. 2009 18:16

asymptoty: je potreba spocitat limity v nule (bod nespojitosti) a v nekonecnu (asymptoty jsou totiz vodorovne)
S nekterymi dalsimi kroky pomuze MAW - zadejte si tam svoji funkci a treba Vam to bude stacit.

bentrix · 11. 01. 2009 18:25

↑ kaja.marik:
graf mi udelal pocitac , me to prave pořad vychází divně nemam moc dobrou hlavu na matiku. mohli byste mi prosim vypocitat aspon ty asymptoty?? ty mi prave vychazej porad nak podivne ty derivace celkem davam ale ty asymptoty mi porad nejdou. :(

bentrix · 11. 01. 2009 18:27

↑ halogan:
ja si prave myslim ze s osou y ma prusecik v bode ln 4

halogan · 11. 01. 2009 18:29

S osou y to nemůže mít průsečík, protože bod [0; f(0)] neexistuje.

bentrix · 11. 01. 2009 18:32

↑ halogan:
aha tak dik jen bych fakt potreboval ty asymptoty byl bych vam vdecnej

bentrix · 11. 01. 2009 18:34

ja su kokot hele ja to zblbnul tuhle funkci ma potreboval bych teda funkci: g(x)=ln(4-xna druhou) sorry s touhletou bych potreboval pomoct ja su vul

halogan · 11. 01. 2009 18:48

$y = \ln {4x^2} \nl y' = 8x \cdot \frac{1}{4x^2} = \frac{2}{x} \nl y'' = \frac{-2}{x^2}$

bentrix · 11. 01. 2009 18:55

dik a ty prusečiky budou tedy pro y (0,ln4)?? , a pro x (+-2,0)??

halogan · 11. 01. 2009 19:06

Průsečík s y ani tato fce nemá, protože ln 0 prostě nemá řešení v R.

Pro průsečík s x řešíš následující rovnici:
$0 = \ln 4x^2 \nl 4x^2 = 1 \nl x^2 = \frac{1}{4} \nl |x| = \frac{1}{2} \nl x = \pm \frac{1}{2}$

bentrix · 11. 01. 2009 19:20

no mě to vyhazuje pořád tento graf

halogan · 11. 01. 2009 19:26

Mně mendelu kreslí

kaja.marik

↑ bentrix:
"to" je Derive?
Ten graf je spatne. Zkuste SAGE a prikazy
P=plot(log(4*x^2),(x,-6,6))
show(P)

bentrix · 11. 01. 2009 19:41

↑ kaja.marik:

no me ten muj graf vyhodila i tato stranka
http://wood.mendelu.cz/math/maw/graf/gr … funkce=log((4-(x^2)))+&xmin=-5&xmax=5&ymin=-10&ymax=10&naturallog=1&logbase=3&tlacitko=Odeslat
a nevite ty asympptoty?? me to porad nejde :(

kaja.marik

Halogan kreslil a resil ln(4*x^2) a to je neco jineho nez ln(4-x^2)
vsiml jsem si toho az ted.
I ten muj prikaz pro sage potrebuje opravit.
asi se vyplati psat 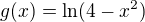$g(x)=\ln(4-x^2)$ a ne "g(x)=ln(4-xna druhou) ", pak k takovym nedorozumenim nebude dochazet

bentrix · 11. 01. 2009 19:56

↑ kaja.marik:
tak sory ale kdyz se vykresli tento graf tak prusecik osou y je v ln 4 a s osou x √3 a -√3. a nevedel bys ty asymptoty??

halogan · 11. 01. 2009 20:02

↑ bentrix:

OMLOUVÁM SE! Má nepozornost. Přehlédl jsem se. Mohl jsi mě na to upozornit, když jsi viděl můj výpočet, abychom toto nedorozumění ukončili dříve.

No to je jedno. Průsečíky máš tedy správně.

A derivace:
$y = \ln(4-x^2) \nl y' = -2x\cdot \frac{1}{4-x^2} = \frac{2x}{x^2 - 4} \nl y'' = \frac{2\cdot(x^2 - 4) - 2x\cdot(2x)}{(x^2 - 4)^2} = \frac{-2\cdot(x^2 + 4)}{(x^2 - 4)^2}$

bentrix · 11. 01. 2009 20:53

no ja kdyz močítam limitu x=2

vyde 0 a
vyde -∞

halogan · 11. 01. 2009 21:03

a proč zrovna u dvojky? Limita pro dvojku zprava ani neexistuje, protože Df = (-2; 2)

Navíc počítáš limitu pro špatnou funkci, chybí ti tam logaritmus.

bentrix

↑ halogan:
no ja sem to blbe opsal a teda pro jakou limitu bych to mel pocitat ?? ∞??
ted sem pocital asymptotu se smernici pro +∞,-∞ a vyslo mi 0

halogan · 11. 01. 2009 22:18

Hledej limitu pro dvojku zleva a pro -2 zprava. Pokud vyjdou +-oo, tak tam bude limita bez smernice.

andrééé · 12. 01. 2009 20:47

Cau mohli by jste mi nekdo helfnout s timto prikladem?potrebuji spocitat 1. a 2. derivaci funkce: y = x * (1 - x)^(1/3).Dikec moc...

halogan · 12. 01. 2009 21:06

↑ andrééé:
A k čemu jsi se dostal? Ať najdeme tvoji chybu

$y = fg \nl y' = f'g + fg' \nl$

Problém tady bude asi (1-x)^{1/3}. Derivuje se to jako složená funkce.

andrééé · 13. 01. 2009 16:17

ja z toho mam vypočitat celej prubeh fce a vysledku mam asi deset:)) kazdej jinak a vsechny blbe

Matematické Fórum

#1 11. 01. 2009 18:10

Průběh funkce

#2 11. 01. 2009 18:15

Re: Průběh funkce

#3 11. 01. 2009 18:16

Re: Průběh funkce

#4 11. 01. 2009 18:25

Re: Průběh funkce

#5 11. 01. 2009 18:27

Re: Průběh funkce

#6 11. 01. 2009 18:29

Re: Průběh funkce

#7 11. 01. 2009 18:32

Re: Průběh funkce

#8 11. 01. 2009 18:34

Re: Průběh funkce

#9 11. 01. 2009 18:48

Re: Průběh funkce

#10 11. 01. 2009 18:55

Re: Průběh funkce

#11 11. 01. 2009 19:06

Re: Průběh funkce

#12 11. 01. 2009 19:20

Re: Průběh funkce

#13 11. 01. 2009 19:26

Re: Průběh funkce

#14 11. 01. 2009 19:28 — Editoval kaja.marik (11. 01. 2009 19:28)

Re: Průběh funkce

#15 11. 01. 2009 19:41

Re: Průběh funkce

#16 11. 01. 2009 19:47 — Editoval kaja.marik (11. 01. 2009 19:51)

Re: Průběh funkce

#17 11. 01. 2009 19:56

Re: Průběh funkce

#18 11. 01. 2009 20:02

Re: Průběh funkce

#19 11. 01. 2009 20:53

Re: Průběh funkce

#20 11. 01. 2009 21:03

Re: Průběh funkce

#21 11. 01. 2009 21:08 — Editoval bentrix (11. 01. 2009 21:09)

Re: Průběh funkce

#22 11. 01. 2009 22:18

Re: Průběh funkce

#23 12. 01. 2009 20:47

Re: Průběh funkce

#24 12. 01. 2009 21:06

Re: Průběh funkce

#25 13. 01. 2009 16:17

Re: Průběh funkce

Zápatí