Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Pevný bod monotónního zobrazení (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 06. 2013 00:05
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Pevný bod monotónního zobrazení
Ahoj,
nechť množina M je lineárně uspořádaná a nechť má vzhledem k tomuto uspořádání nejmenší a největší prvek. Nechť f je (ostře) rostoucí zobrazení z M do M (tj. pro x<y je f(x)<f(y)). Dokažte nebo vyvraťte, že f má pevný bod - tj. existuje c takové, že f(c)=c.
"Máte úhel beta." "No to nemám."
Offline
- (téma jako vyřešené označil(a) check_drummer)
#2 29. 06. 2013 19:53
#3 29. 06. 2013 23:40
Re: Pevný bod monotónního zobrazení
Ahoj ↑ check_drummer:,
pozri si napr toto http://en.wikipedia.org/wiki/Fixed_poin … ematics%29
Odpoved na tvoju otazku je ako napisal kolega↑ OiBobik:, vseobecne nie.
Ale za urcitych hypotez, odpoved je kladna.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 30. 06. 2013 09:32 — Editoval check_drummer (30. 06. 2013 09:33)
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Pevný bod monotónního zobrazení
↑ OiBobik:
Ahoj, díky, to je pravda. Já jsem spíš přemýšlel o takových množinách, ze kterých nedovolíme "vyndavat" prvky - ovšem toto bych musel nějak striktně podchytit (např. pomocí nějaké souvislosti, spojitosti, apod.). (A somozřejmě jsem to měl uvést.) Pro začátek se ptejme, zda existuje zobrazení f bez pevného bodu pro ![kopírovat do textarea $M:=[0;1] \cap \mathbb{Q}$](/mathtex/3d/3d90982d53c53f84d699d58d12d9f835.gif) . Pro
. Pro ![kopírovat do textarea $M:=[0;1]$](/mathtex/68/68eac359452a88b7de5a927f2728f5be.gif) si myslím, že pevný bod existuje vždy - důkaz by vhodně využil existence suprema každé podmnožiny M - ovšem pokud budeme jen v racionálních číslech, není důkaz (ne)existence pevného bodu na první pohled zřejmý (alespoň pro mě).
si myslím, že pevný bod existuje vždy - důkaz by vhodně využil existence suprema každé podmnožiny M - ovšem pokud budeme jen v racionálních číslech, není důkaz (ne)existence pevného bodu na první pohled zřejmý (alespoň pro mě).
Napadlo mě zkoumat f(M),f(f(M)),..., ovšem tato posloupnost nemusí konvergovat k jednobodové množině (myslím si).
"Máte úhel beta." "No to nemám."
Offline
#5 30. 06. 2013 18:00
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Pevný bod monotónního zobrazení
↑ check_drummer:
Co se tyce prikladu ![kopírovat do textarea $[0,1]\cap \mathbb{Q}$](/mathtex/05/05f1721beb2b0e072b5173b0689a64af.gif) , staci vzit funkci
, staci vzit funkci 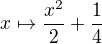 - ta ma potencialni pevny bod iracionalni, takze skutecne nema pevny bod.
- ta ma potencialni pevny bod iracionalni, takze skutecne nema pevny bod.
Myslim, ze priklad ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) uz mit vzdy pevny bod bude.
uz mit vzdy pevny bod bude.
Podobne si myslim, ze pevny bod bude existovat, kdykoli to bude dobre usporadani.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#6 01. 07. 2013 17:13 — Editoval OiBobik (01. 07. 2013 17:15)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Pevný bod monotónního zobrazení
Pridavam jeste dukaz tech dvou domnenek:
Oznacme 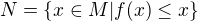 a
a 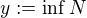 .
.
Buno o  predpokladejme, ze krajni body nejsou pevne body - pak je jiste
predpokladejme, ze krajni body nejsou pevne body - pak je jiste  neprazdna.
neprazdna.
A) Pripad ![kopírovat do textarea $M=[0,1]$](/mathtex/6b/6b4ccad846f81150ac6061c8608a01a9.gif) : Tvrdime, ze
: Tvrdime, ze :
:
Necht ne, tedy  . Pak z vlastnosti infima existuje
. Pak z vlastnosti infima existuje 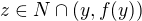 . Tedy z
. Tedy z  , zaroven vsak
, zaroven vsak  , tedy
, tedy  . To je spor.
. To je spor.
B) At uz jde o dobre usp. nebo o pripad ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) , diky A) mame, ze
, diky A) mame, ze 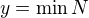 . Tedy
. Tedy  . Pro spor predpokladejme, ze
. Pro spor predpokladejme, ze  . Pak na jednu stranu,
. Pak na jednu stranu,  , tedy
, tedy  . Na druhou stranu,
. Na druhou stranu,  a
a  je rostouci, tedy
je rostouci, tedy  . To je spor. Nutne tedy nastava rovnost.
. To je spor. Nutne tedy nastava rovnost.
Pozn: zda se mi, ze stejny dukaz projde i pro neostre verze, tj pro neklesajici funkci.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Pevný bod monotónního zobrazení (TOTO TÉMA JE VYŘEŠENÉ)
![kopírovat do textarea $M:=[0,1]\setminus \{\frac{1}{2}\}$](/mathtex/0d/0d52a5a98b4112ce8dd5a789319be287.gif) s obvyklým uspořádáním. Pak zobrazení
s obvyklým uspořádáním. Pak zobrazení  nemá pevný bod - zkrátka proto, že jsme jej "vyndali". :))
nemá pevný bod - zkrátka proto, že jsme jej "vyndali". :))